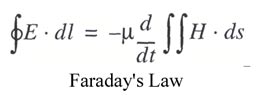Faraday's Law: Difference between revisions
No edit summary |
No edit summary |
||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
== Faraday's Law | == Faraday's Law == | ||
[[Image:Faraday's Law.jpg|thumb| | [[Image:Faraday's Law.jpg|thumb|right|Faraday’s Law shows how a changing magnetic field, H, can create an electric field, E.]] | ||
The second of the four [[Maxwell's Equations|Maxwell’s Equations]] is called Faraday’s Law, named after the English physicist [[Michael Faraday|Michael Faraday]]. This equation describes how a changing magnetic field produces an electric field and is almost an exact mirror image of Ampère’s Law. As in Ampère’s Law, E represents the electric field and H represents the magnetic field. Faraday first described this law in practical terms, then Maxwell translated the idea into this equation. | The second of the four [[Maxwell's Equations|Maxwell’s Equations]] is called Faraday’s Law, named after the English physicist [[Michael Faraday|Michael Faraday]]. This equation describes how a changing magnetic field produces an electric field and is almost an exact mirror image of [[Ampere's Law|Ampère’s Law]]. As in [[Ampere's Law|Ampère’s Law]], E represents the electric field and H represents the magnetic field. [[Michael Faraday|Faraday]] first described this law in practical terms, then [[James Clerk Maxwell|Maxwell]] translated the idea into this equation. | ||
The left hand side (that is, left of the equal sign) of this equation is just like the left hand side of Ampère’s Law only with an electric field instead of magnetic field. Just as with Ampère’s Law, you can select any closed curve at all (note the same little circle in the very first symbol), and add the electric field that is parallel to the curve over the entire length of the curve. As before, all electric field perpendicular to the curve is ignored. | The left hand side (that is, left of the equal sign) of this equation is just like the left hand side of Ampère’s Law only with an electric field instead of magnetic field. Just as with Ampère’s Law, you can select any closed curve at all (note the same little circle in the very first symbol), and add the electric field that is parallel to the curve over the entire length of the curve. As before, all electric field perpendicular to the curve is ignored. | ||
| Line 15: | Line 15: | ||
Notice that the right hand side of the equation also contains the Greek letter µ (spelled “mu” and pronounced “mew”). This has to do with substances like iron. Iron is easily affected by a magnetic field and has a large µ. Mu is the permeability of the substance, which is a measure of its susceptibility to magnetic fields. A large µ magnifies the effect of the changing magnetic field (right hand side in Faraday’s Law). This is why iron is often used in magnets. If you use iron with µ of 80, then your magnet is 80 times stronger and your generator is 80 times more powerful. | Notice that the right hand side of the equation also contains the Greek letter µ (spelled “mu” and pronounced “mew”). This has to do with substances like iron. Iron is easily affected by a magnetic field and has a large µ. Mu is the permeability of the substance, which is a measure of its susceptibility to magnetic fields. A large µ magnifies the effect of the changing magnetic field (right hand side in Faraday’s Law). This is why iron is often used in magnets. If you use iron with µ of 80, then your magnet is 80 times stronger and your generator is 80 times more powerful. | ||
The order can be reversed and, thus, voltage can be used to make a changing magnetic field. Take an electric generator and put a voltage on it. The magnet inside will start spinning. This is exactly how a motor works. Faraday’s Law says that if you want the motor to spin faster, just turn up the voltage. If you picture an electric fan, the higher the voltage applied, the faster the motor works, and the faster the blades turn. Of course, this stops working when the wire in the motor melts. But even then, Faraday’s Law still works, anywhere, anytime, for any curve. | The order can be reversed and, thus, voltage can be used to make a changing magnetic field. Take an electric generator and put a voltage on it. The magnet inside will start spinning. This is exactly how a motor works. Faraday’s Law says that if you want the motor to spin faster, just turn up the voltage. If you picture an electric fan, the higher the voltage applied, the faster the motor works, and the faster the blades turn. Of course, this stops working when the wire in the motor melts. But even then, Faraday’s Law still works, anywhere, anytime, for any curve. | ||
[[Category: | [[Category:Fields,_waves_&_electromagnetics]] | ||
[[Category:Electromagnetics]] | |||
[[Category:Electromagnetic_fields]] | |||
[[Category:News]] | |||
[[Category:People_and_organizations]] | |||
[[Category:Scientists]] | |||
[[Category:Scientific_tools_and_discoveries]] | |||
[[Category:Mathematics]] | |||
[[Category:Calculus]] | |||
Revision as of 13:40, 16 May 2012
Faraday's Law
The second of the four Maxwell’s Equations is called Faraday’s Law, named after the English physicist Michael Faraday. This equation describes how a changing magnetic field produces an electric field and is almost an exact mirror image of Ampère’s Law. As in Ampère’s Law, E represents the electric field and H represents the magnetic field. Faraday first described this law in practical terms, then Maxwell translated the idea into this equation.
The left hand side (that is, left of the equal sign) of this equation is just like the left hand side of Ampère’s Law only with an electric field instead of magnetic field. Just as with Ampère’s Law, you can select any closed curve at all (note the same little circle in the very first symbol), and add the electric field that is parallel to the curve over the entire length of the curve. As before, all electric field perpendicular to the curve is ignored.
The right hand side of the equation looks complicated, but the idea is simple. It says to calculate first the total magnetic field “flowing” though the same curve used for the left hand side. This equation works for any closed curve. You just have to use the same curve on both sides of the equation. Imagine a surface whose boundary is the curve used on the left hand side. Then Faraday’s Law says that the magnetic flux through this surface is related in a particular way to the electric field around the curve.
Next, look at the d/dt. This looks like a fraction, but it isn’t. It is called a time derivative, and is saying that we are not interested in the actual value of the total magnetic field that is “jumping through the hoop,” but we are interested in how fast the total magnetic field is changing. We could have a huge magnetic field, but if it stays the same all the time, we don’t care about it. If we were to actually calculate a number for this term, the faster the magnetic field is changing, the bigger the result.
Faraday’s Law says that when you have a changing magnetic field (right hand side), it generates an electric field (left hand side). In addition, the faster the magnetic field changes, the bigger the electric field. This is how an electric generator works. Spinning a magnet makes a rapidly changing magnetic field. This changing magnetic field generates an electric field, or voltage. If you want more voltage, just spin the magnet faster. This is how nearly all electricity in the world is generated.
Notice that the right hand side of the equation also contains the Greek letter µ (spelled “mu” and pronounced “mew”). This has to do with substances like iron. Iron is easily affected by a magnetic field and has a large µ. Mu is the permeability of the substance, which is a measure of its susceptibility to magnetic fields. A large µ magnifies the effect of the changing magnetic field (right hand side in Faraday’s Law). This is why iron is often used in magnets. If you use iron with µ of 80, then your magnet is 80 times stronger and your generator is 80 times more powerful.
The order can be reversed and, thus, voltage can be used to make a changing magnetic field. Take an electric generator and put a voltage on it. The magnet inside will start spinning. This is exactly how a motor works. Faraday’s Law says that if you want the motor to spin faster, just turn up the voltage. If you picture an electric fan, the higher the voltage applied, the faster the motor works, and the faster the blades turn. Of course, this stops working when the wire in the motor melts. But even then, Faraday’s Law still works, anywhere, anytime, for any curve.