ENIAC: Difference between revisions
No edit summary |
m (Text replace - "[[Category:Components,_circuits,_devices_&_systems" to "[[Category:Computers and information processing") |
||
| Line 23: | Line 23: | ||
The architecture of the Eniac was base 10, not the modern day base 2 logic, with manual table sets to solve the second order differential equations for ballistic trajectories. | The architecture of the Eniac was base 10, not the modern day base 2 logic, with manual table sets to solve the second order differential equations for ballistic trajectories. | ||
[[Category: | [[Category:Computers and information processing]] | ||
[[Category:Logic_devices]] | [[Category:Logic_devices]] | ||
[[Category:Logic_arrays_&_devices]] | [[Category:Logic_arrays_&_devices]] | ||
Revision as of 15:44, 22 July 2014
ENIAC
The ENIAC (Electronic Numerical Integrator and Computer), built in the years 1943 to 1946, is widely regarded as the first general-purpose electronic digital computer. The military needed ENIAC for the calculation of ballistic tables. These were numerical tables used by artillery personnel that related how the range of a particular gun depended upon the type of shell that was fired, the charge of the propellant, the angle of elevation, and, in some cases, the meteorological conditions. New guns, new shells, and new propellants required new tables, and the calculation of a table involved solving a complicated set of differential equations. This was a major task that was carried out for the U.S. Army mainly at the Ballistic Research Laboratory of the Aberdeen Proving Ground in Maryland.
When the United States entered World War II, the Moore School of Electrical Engineering at the University of Pennsylvania undertook the building of an electronic computing machine for the Ballistic Research Laboratory. The principal designers were J. Presper Eckert, an electrical engineer at the Moore School, and John Mauchly, a physicist who had become interested in calculating devices from his efforts to apply statistical methods to meteorological data. Eckert and Mauchly designed the machine to compute ballistic tables, but recognized that it could be applied to a very wide range of problems.

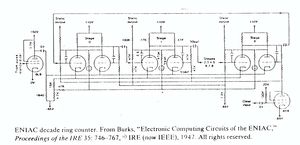
ENIAC contained 20 electronic accumulators, each of which could store a 10-digit decimal number. Its logic circuits were also electronic. The sequence of operations was set by the placement of patchcords in plugboards. ENIAC also had read-only memory of about 300 numbers, which were entered by turning switches. An IBM card reader and an IBM cardpunch provided input and output. All together there were 18,000 tubes, 70,000 resistors, 10,000 capacitors, 1500 relays, and 6000 manual switches. This equipment consumed 140 kW of power and filled a room 20 feet by 40 feet.
Work on the ENIAC began in 1943 and proceeded rapidly, but the war ended before the machine was fully operational. In December 1945, it solved a problem for the hydrogen-bomb project, and on 15 February 1946 at the Moore School, it was formally dedicated.
The computer was extremely influential in the subsequent growth of electronic computing. Many of those involved in building the ENIAC, including John Mauchly, Presper Eckert, John von Neumann, Herman Goldstine, and Arthur Burks, played major roles in the larger story of computer development. The expertise gained in the project was widely shared through publications, site visits, and a course on electronic computing offered by the Moore School in the summer of 1946.
The ENIAC Museum is on the ground floor of the Moore School Building, 200 South 33rd Street, of the University of Pennsylvania. This museum is located just 20m away from the very original location of the Eniac installation, in the student lounge area. The ENIAC Museum contains four of the original 40 panels of the machine, as well as many other artifacts. Mitchell Marcus, professor of computer science, and Paul Schaffer, curator of the ENIAC Museum in 2009.
The architecture of the Eniac was base 10, not the modern day base 2 logic, with manual table sets to solve the second order differential equations for ballistic trajectories.