The encryption war of WWII: the Enigma encryption machine: Difference between revisions
No edit summary |
No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 149: | Line 149: | ||
As the fate of battling the Enigma changed hands from Polish intelligence to British intelligence, the rate of evolution on both sides of the communication battle only started to evolve more rapidly. Even with the founding of Bletchley Park, Britain’s new headquarters for code and cipher breaking which eventually housed up to seven-thousand workers, quicker methods for solving the Enigma’s daily keys was always an ever-pressing issue. And to make matters worse, the methods coined by Rejewski for determining the daily key, which heavily relied on the use of the doubly encrypted message key, saw the possibility of becoming obsolete. | As the fate of battling the Enigma changed hands from Polish intelligence to British intelligence, the rate of evolution on both sides of the communication battle only started to evolve more rapidly. Even with the founding of Bletchley Park, Britain’s new headquarters for code and cipher breaking which eventually housed up to seven-thousand workers, quicker methods for solving the Enigma’s daily keys was always an ever-pressing issue. And to make matters worse, the methods coined by Rejewski for determining the daily key, which heavily relied on the use of the doubly encrypted message key, saw the possibility of becoming obsolete. | ||
It would be the famous mathematician and computer scientist Alan Turing, standing on the work laid down by Rejewski and the Polish, who would discover a weakness in the Enigma’s application so significant, that no German renovations to the standing machine would be able to prevent. At Bletchley Park, Turing was eventually given the task of exploring alternatives to Rejewski’s methods of finding the daily key, as British intelligence had the foresight to assume that the message key procedure, which revealed clues about the daily key, would not be around forever. | It would be the famous mathematician and computer scientist [[Alan Turing]], standing on the work laid down by Rejewski and the Polish, who would discover a weakness in the Enigma’s application so significant, that no German renovations to the standing machine would be able to prevent. At Bletchley Park, Turing was eventually given the task of exploring alternatives to Rejewski’s methods of finding the daily key, as British intelligence had the foresight to assume that the message key procedure, which revealed clues about the daily key, would not be around forever. | ||
[[Image:Turing00.jpg]] | [[Image:Turing00.jpg]] | ||
| Line 165: | Line 165: | ||
''1.Singh, S., (2000). The Code Book: The science of secrecy from ancient Egypt to quantum cryptography. US: Random House Inc.'' | ''1.Singh, S., (2000). The Code Book: The science of secrecy from ancient Egypt to quantum cryptography. US: Random House Inc.'' | ||
[[Category: | [[Category:Computers and information processing|Enigma]] [[Category:Information theory|Enigma]] [[Category:Codes|Enigma]] [[Category:Cryptography|Enigma]] [[Category:Decoding|Enigma]] [[Category:Encoding|Enigma]] | ||
[[Category: | |||
[[Category:Codes]] | |||
[[Category:Cryptography]] | |||
[[Category:Decoding]] | |||
[[Category:Encoding]] | |||
Revision as of 14:50, 29 March 2012
Brief Overview
I’m a student in the History of Computing class at San Jose State University ([1]). This is a work in progress that will turn into a final article by the end of the semester in December of 2011. I welcome your comments and advice.
I am developing a java simulation of one of the encryption machines used in World War II by the Nazi military--The Enigma. During my research and development, I have been learning a lot about the disciplined effort that was made toward creating this encryption system that was (presumably) unbreakable; but this task at hand calls for the mentioning of even greater events happening simultaneously. The efforts of the mathematicians and computer scientists all around Europe, namely Poland, France, and the British intelligence at Bletchley Park unarguably changed the course of WWII.
Upon completion of my Enigma simulator, I want to apply what I have learned about the machine's construction and use in war time and apply it to the perspective of the allied forces. I intend to define how Bletchley Park scientists determined their decryption algorithms and more importantly draw a relationship to the magnitude of their efforts in both revolutionary thinking in the field of computers as well as respective technological growth.
By December I intend to have a working simulation of the Enigma encryption machine along with algorithms derived from computer scientists at the time that can be applied to the simulator for decryption. Like with any history article, I intend to provide a solid historical grounding in the events which incited these technologies.
"Necessity is the mother of invention."
My Enigma Simulator
The package of source code for my Enigma Simulator can be obtained from the free file hosting site found at this link:
www.filedropper.com/enigmasimulatorsource
Included in the .zip file are all of the .java source files, along with their respective .txt files. Compiling and running the EnigmaDemo.class file will initiate the simulator.
>EnigmaDemo.java
>Enigma.java (with documentation)
>Rotor.java (with documentation)
>Reflector.java (with documentation)
>EModel.java
>EFrame.java
>SettingPanel.java
Mechanizing Encryption
In 1923 the British Royal Navy produced their official historical account of World War I. In this account, along with Winston Churchill’s The World Crisis, also published during the same year, it was openly released for the first time that the Allies’ advantages over the Germans were largely due to the acquisition of German codebooks and the decryption efforts of the British and French intelligence Bureaus (Churchill, 2005)1. This is undoubtedly true in many respects, ranging from the outcomes of naval battles at sea to the ultimate fact that Allied intelligence reduced the scale and duration of the war as a whole. In fact, the advantages provided by successful allied intelligence played such a large role during the course of WWI that up until the release of these publications, it was considered by French and British entities alike that such information should be kept secret from Germany at all costs.
Back in early 1917, despite German actions to go forward with their policy on unrestricted submarine warfare, the United States would have continued to remain neutral were it not for Germany’s incriminating plans against the U.S. that were discovered by British intelligence. It was Germany’s Foreign Minister, Arthur Zimmerman and his encrypted message to Mexico City that would change America’s mind, and consequently change the course of the war.
However during this dramatic point, even after Germany recognized that their communications had been discovered, the encryption security of such communications was never brought to Germany’s attention. It was indeed the British cipher breakers who discovered Germany’s intentions first, having decoded the Zimmerman telegraph weeks after its interception, but it was of great importance to the Allies that Germany never find out that their encryption security had been compromised for fear that they might improve their methods. Instead, this achievement by Britain’s Cipher Bureau and Allied efforts was masked by a constructed news story indicating that the famous Zimmerman telegraph was actually stolen from Mexico City only after its presumably safe travel. Almost seven years later in 1923, upon Britain’s release of their code breaking victories, Germany realizes its confidence in communications security had been misplaced.
At this point in time, initial versions of the Enigma machine had already been built and had seen only failure in virtually all markets in Germany during the six years since its inception. Its inventor, Arthur Scherbius, had a keen interest in WWI cryptography—and more specifically—modifying the paper-and-pencil methods of the 19th century to utilize 20th century mechanized technology. Though the Enigma eventually underwent many modifications after its adoption by the German military, its remarkable design was founded on the ideas of Scherbius and improvements to the cipher failures of the past through mechanization.
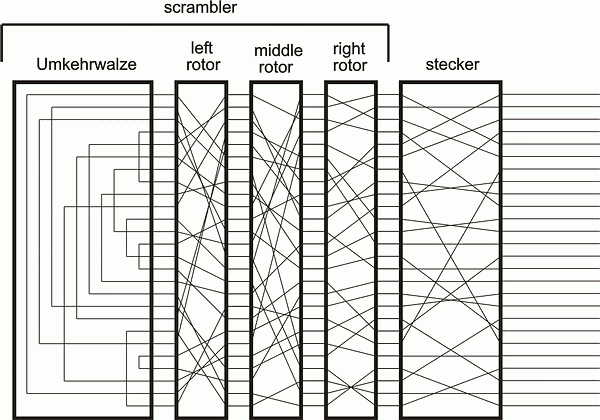
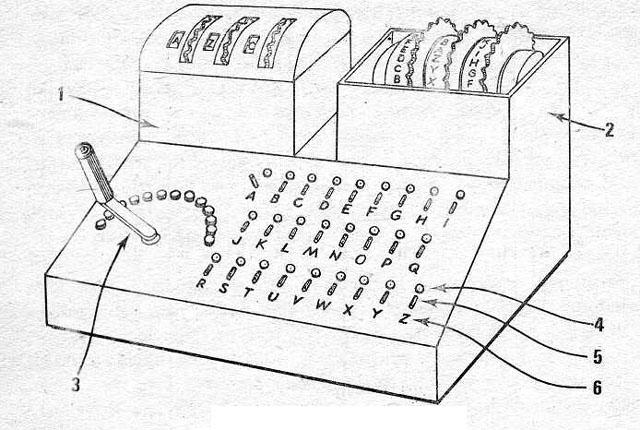
Scherbius’s design for the encryption procedure of the Enigma consisted of three independent components. A keyboard produced electrical signals which would pass as inputs through one of 26 different wires (A-Z) through the first component known as the plugboard or Steckerbrett. The plugboard acted as a redirector of input and output from the rest of the machine and consisted of an array of 26 dual-pass sockets, each representing a character of the alphabet. If a plug was connected into one socket, say ‘F’ for example, and the other end of the cable was inserted into the socket for ‘L’, a signal passing through one of the wires designated for either ‘F’ or ‘L’ would switch to its respective other upon passing through the plugboard. This component served as a simple substitution function for various input and could support up to 13 cables inserted in any way into the 26 sockets. Signals passing through the plugboard then come in contact with the next enciphering component—the rotor system.
A rotor by itself is responsible for another letter-to-letter substitution. Twenty-six electrical contacts on one face of the disk connect through internal wiring to 26 other contacts on the other side in a seemingly random relationship, changing the course of the input signal’s path through the machine. Scherbius’s design utilized three of these rotors, all with different internal wiring relationships, connected in series to provide three layers of substitution before exiting as output. However, arguably the most interesting thing about the Enigma machine is that these rotors would independently rotate at certain stages of enciphering a message so the cipher would constantly cycle through sets of substitution alphabets. How many substitution alphabets were possible as a result of this rotor series mechanism? Every time input is sent from the keyboard, the rightmost rotor in the machine would “step” by 1/26th of a rotation, essentially changing connections of each input lead of the rotor to the next output lead from the plugboard, and changing connections of each output lead of the rotor to the next input lead of its neighboring rotor. By the time the rightmost rotor makes a full rotation (26 keystrokes from the keyboard) the neighboring rotor to the left will be triggered to step once. So even though the rotor on the right has returned to its original substitution alphabet (orientation of its internal wiring relative to its input), the middle rotor has changed its orientation and so the substitution which spans both rotors is still completely different; and as the middle rotor comes to a full rotation, this consequently triggers a step in the left most rotor. To put this in perspective, an operator of the Enigma would have to depress 26*26*26 = 17,576 keys to arrive back at the original substitution alphabet that the machine started at, roughly more than six pages filled with encrypted letters.
The occurrence of a rotor step (other than the right most rotor which steps after every keystroke) is a result of the rotational orientation of the rotor to its right. This is caused by a detachable component of the rotor that could be referred to as the ring. The rotor’s ring—which is essentially a metal ring which fits around the outside edge of the rotor—has letter engravings around its circumference corresponding to the 26 internal wirings attached to each set of electrical leads. At a designated letter on each ring was a “notch” which when oriented in a certain position within the Enigma would trigger a neighboring rotor to step. The significance of the detachable property of this ring is that its notch (and the letter engravings corresponding to each wire connection of the rotor) could be adjusted, adding yet another variable element to the enciphering behavior of the machine.
Another ingenious property of these rotors is their compatibility with the Enigma in any arrangement. Any of the rotors labeled I, II, and III could be inserted into any of the three rotor slots; and because these three rotors were all different from each other in terms of internal wiring, each arrangement created a completely new set of substitution alphabets. Imagine now that the Enigma operator is encoding the same letter ‘A’ over and over. As outlined above, this would create a pattern that wouldn’t repeat itself until enciphering 17,576 ‘A’s, and furthermore this 17,576 letter long pattern would be completely different under any other arrangement of the three rotors.
During the post-WWI era, as exemplified by the events of the Zimmerman telegram decryption, cryptographers were constantly losing ground to cipher breakers and cryptanalysts. Creating strong enough ciphers was simply too inefficient, especially in the context of wartime, as they required very large sets of randomly generated substitution alphabets. Thus, achieving as many different cipher possibilities as what was now capable with the Enigma was extremely rare, but not impossible. In fact, it was the Americans during the end of WWI who gave birth to the idea that if a unique, randomly generated substitution alphabet was used for each letter in a ciphertext, decryption of such a ciphertext would be theoretically impossible if the cipher key was kept out of the hands of a code breaker. Without repeating the way a plaintext letter was mapped to its respective ciphertext, such an algorithm is virtually patternless and thus mathematically proven to be unbreakable without knowledge of what substitutions comprised the cipher.
However, this groundbreaking method came with its drawbacks. Before the use of Enigma-like machines for producing substitution alphabets, cryptographers using this system had to rely on large tables filled with hundreds of randomly generated letters. A long string of these letters with length equal to that of the plaintext to be encrypted would be taken from a given table and would serve as the basis for the polyalphabetic substitution. U.S. Army cryptographer Major Joseph Mauborgne coined this idea with the creation of the one-time pad which was essentially a thick stack of sheets with such randomly generated tables printed on them (Singh, 2000)2. If such a pad was produced and distributed to those responsible for sending and receiving encrypted messages, a key for decryption would never have to be exchanged. Instead, the only information that a cryptographer would have to include along with an enciphered message would be the starting position of the string of letters found on the first sheet of the one-time pad that a message receivers could refer to on their own one-time pad table. Such extra information would be useless to an outside interceptor without access to the random table that was used to produce the message, and because each sheet was intended to be discarded after use (hence the name “one-time pad”), the possibility of recognizing patterns in an encrypted message was nonexistent.
Even though the one-time pad offered this seemingly impeccable communication security, the cost and impracticality of creating such pads hindered their usefulness in many different contexts. For example in the heat of a war, if a one-time pad was seized by an enemy interested in decrypting messages, virtually all identical pads produced at the same time would be rendered useless because the message key could then be determined by those with access to the table of letters that were used. Such valuable references obviously could not afford to be on the battlefront. Furthermore, the production of these pads was neither timely nor cost-effective because the procedures for producing truly random sequences of letters (virtually free of any pattern) requires the reliance on processes found in nature, not human design (Rabah, 2005)3.
Scherbius’s rotor design offered a timely compromise to the drawbacks of the one-time pad by mechanizing the selection of alphabet substitutions. The Enigma produces an encryption cipher in the same fashion as the one-time pad process because each encrypted letter of a cipher text is produced by a unique and different orientation of the rotors’ internal wiring, with no repeated pattern as long as the message does not exceed 17,576 characters. Like the starting position on a one-time pad table, the initial setup of the Enigma’s rotors (along with the plugboard configuration) determines the entire cipher key for a translated message. This eliminated the need for mass-producing costly random letter tables and mitigated the vulnerability of decrypted messages in the event of a stolen Enigma. A captor of a machine would not be able to decrypt any given message without the additional knowledge of how the machine that produced such messages was initially set up. Having a machine provide the algorithm for encryption also increased the convenience for the cryptographer. Although heavy, the Enigma could be used in the most pressing of situations, creating messages on the fly and with some reductions to human error.
Decryption was just as convenient. One of the modifications to Scherbius’s design was an unchanging rotor-like component called a reflector, installed at the receiving end of the leftmost rotor. Although this component did not change states like the rotors did through stepping, it provided an additional substitution layer and something much more convenient. The reflector’s internal wiring would receive the signal produced by the leftmost rotor and would send the signal back through another terminal of the same rotor, reversing the path of the input. By doing this, an input was not only doubly-encrypted by the rotor mechanism, but the unchanging characteristic of the reflector ensured that inputs and outputs through the Enigma were reciprocals of each other. That is, if an Enigma at an arbitrary initial setup mapped the letter ‘A’ to the cipher letter ‘B’, another Enigma starting at the same setup would produce the cipher letter ‘A’ from the letter ‘B’. This allowed almost anyone with granted knowledge of the initial setup of the producing machine to decrypt ciphertext simply by sending each character through their own machine; operators responsible for sending top-secret messages no longer had to be as qualified or knowledgeable of cryptographic characteristics.
Like with any compromise however, these characteristics of the Enigma also provided security drawbacks. These draw backs will be discussed in later sections. One thing that should be noted about this transition to a mechanized way of encryption is the effect it had on many aspects of cryptology’s counterpart—cryptanalysis. Just as the achievements of the allied code breakers of WWI incited the Germans to bolster their communications security, significant advancements in encryption technology forced likewise evolution in the field of conquering these encryption secrets. This is not a unique theme as the ever-nascent battle between code makers and code breakers has existed since the dawn of information sharing, and the dramatic information battle of WWII is one of history’s great examples of this phenomenon.
Annotations and references 1.Churchill, W., (2005). The World Ciris. UK: Simon and Schuster.
Churchill lists many wartime events in which Naval procedures and counter-operations were incited from obtaining intelligence: codebooks, radio/telegraph interception.
2.Singh, S., (2000). The Code Book: The science of secrecy from ancient Egypt to quantum cryptography. US: Random House Inc.
The use of the one-time pad and the tables of randomly generated letter tables was mostly used in producing cipher keys for encrypting messages through the Vigenere cipher, a form of polyalphabetic substitution which relied on a string of characters as a basis for its substitution set. Although Major Mauborgne was not the originator of the randomly generated character set, the one-time pad innovation was largely credited to his introduction in WWI.
3.Rabah, K.V.O., (2005). Implementation of One-Time Pad Cryptography.Information Technology Journal, 4(1) 87-95.
Rabah discusses various methods for creating random and pseudorandom streams of keys. The pseudorandom methods discussed include mathematical algorithms, however these methods are deterministic and not truly random. The random generation used for the production of one-time pad tables relied on natural processes observed in quantum mechanical events.
Emergence of the Military Enigma
After 1923, a very defeated Germany faced a much needed reevaluation of their communications security. Suddenly Scherbius’ encryption machine not only seemed much more valuable to the German military, this new technology also appeared to be the only option for not repeating security pitfalls of the past. In two years, Scherbius’s design went from a seldom used private-enterprise appliance, to a mass produced Government necessity. It is estimated that by the end of the World War II, the number of Enigma machines purchased by the German government had exceeded 30,000 units; and before the war had begun, it was more than just the Germans who realized the potential of this drastic change. (Singh, 2000)1.
After the events of the First World War, it was not a surprise that nations all over Europe maintained a high level of interest in Germany’s telecommunications. So when intercepted German ciphertext suddenly became unsolvable by virtually all outside intelligence entities, it should be expected that solving this new cipher would have taken on quite a high priority among adverse governments—but this was far from the truth. A significantly decreased sense of urgency had settled into the intelligence bureaus of the post-war allied nations. The British-French alliance, despite a complete state of darkness in the new era of Germany’s communications security, still seemed to hold on to a sense of supremacy in the intelligence domain. After all, it was the shared intelligence of these respective bureaus which had nullified the now dated 19th century cipher applications and, before openly publicizing their achievements, managed to keep these advantages completely secret from their enemies. Additionally, in the eyes of the Allies, the Germans stood at the depths of defeat—certainly well off course from posing any grave threat.
However the post-war allies’ sentiments were not universally felt. Poland, achieving its newly-formed independence as a product of The Treaty of Versailles, was dealing the dilemma of quenching the aspirations of their adverse neighbors—Germany and Soviet Russia. It was clear that German resentment as a result of WWI posed a direct threat to the security and jurisdiction of Poland’s newly formed territory; and just was well the Russian Soviets sought to expand their influence across Europe and beyond. Without a doubt, Poland could not afford the leisure of ignoring communications coming from the German military. It was this fear which is later shared across the world during the heat of the Second World War that is possibly the key driving force of history’s cryptanalytic ingenuity.
This is not to say that Poland sparked the Enigma decryption process without the help of allied intelligence. In fact it was only because of French initiatives that the efforts and contributions of the Polish Cipher Bureau (Biuro Szyfrow) had been able to take off—but this process was slow. In 1927, Poland had acquired its first physical look at an Enigma machine. Confiscated through the Warsaw Customs office, the machine was only the commercial version as the German military had not begun using the machine for broadcasting yet. Nevertheless, this discovery would become of obvious importance to the Polish once German encrypted messages began to indicate that the Enigma had begun use for broadcast in July of 1928 (Rejewski, 2005)2. It is because the Polish handled this event with extreme importance that its cipher bureau underwent some significant changes.
It was rarely, if not never the case previously, that machines were being used on such a large scale for keeping communications secure. Up until the transition ushered in by the Enigma machine, a competent cryptographer or code breaker was thought to be a knowledgeable linguist, well-rehearsed in a wide range of classic thought and cultures. That is because of the common knowledge that cipher keys of the time were generated by human creativity. A considerably strong human-made cipher key—at its base—generally consisted of a mix of dated languages, countries, and historical figures. However his new form of encryption was mechanical; solving this new problem of finding cipher patterns in a mechanically produced algorithm would require a mathematical thinker, and the Polish cipher bureau realized this.
A mathematician by the name of Marian Rejewski was first introduced to the cipher bureau in Poland through the cryptography course that the bureau started at the University of Poznan (Kozaczuk, 1984)3. It was at this point which Rejewski, one of the big heroes of the intelligence battle for the allies, would start his path to making the first significant realization about the behavior of the Enigma machine.
In July of 1978, less than two years before Rejewski’s death, he gave his first-hand account in a recorded interview with Richard Woytak on how he went from a University teacher’s assistant, to a part time non-government employee of the cipher bureau, to eventually working on Enigma encryptions in real-time (Kozaczuk, 1984)4. Rejewski’s work had been kept secret from his peers, also working within the bureau, and a majority of the time he became accustomed to working in isolation. Much of Rejewski’s initial work involving the Enigma ciphers was focused on finding the German’s daily key, the dictated initial setup of the Enigma’s rotors, reflector, and plugboard. This daily key was without a doubt the underlying strength of German communications. The sheer amount of possibilities that the key could be were too much for any sort of exhaustive search that would have been available at the time.
Realistically, determining the Enigma’s daily key was the only barrier which prevented the Allies from decrypting the Enigma machine. In 1931, before Rejewski had even started working on Enigma messages, the French Intelligence Agency had acquired comprehensive information on using the military Enigma and implications of the rotors’ internal wiring. This was all thanks to a defecting worker from the Chiffrierstelle, the German agency stationed in Berlin responsible for many operations involving German communications. French secret agents had been able to meet with the much disenfranchised German government official, Hans-Thilo Schmidt, on multiple occasions in order to obtain such valuable information which Schmidt gave up seemingly willingly (Stengers, 2004)5. Despite their contributions however, the French did not hold much value in this recovery. According to French Captain Gustave Bertrand, at the time a Superior of French Intelligence’s foreign code and cipher branch, the intelligence bureau saw the task of discovering Enigma’s baffling daily key as unsolvable, and hence reproducing a military Enigma of their own based on Schmidt’s documents provided virtually no progress in cracking the German ciphers. (Stengers, 2004)6
The perspective on the Enigma’s mysterious daily key was about to change radically in Poland. Even though the French saw little value in the information recovered about the military Enigma, they passed it along to the Polish Cipher bureau where it would eventually fall into the lap of Rejewski and his colleagues, and an exact replica of the machine finally had been made. Soon Rejewski and the other mathematicians at the cipher bureau would be relieved that the efforts of Schmidt and French Intelligence would not have been made in vain. By 1933 and roughly through all of the 1930’s (up until the beginning of 1939), Poland was able to determine the daily keys of almost every message that was intercepted by exploiting a fatal flaw of how Enigma operators sent their messages.
Before any message was sent by an operator, but after the designated key for the day was set up, it was a military standard procedure for all Enigma operators to randomly select three letters as a basis for their own message key—the actual key used to encrypt the message which would follow. These three letters would be typed at the header of the sender’s message and the sending operator would then set his three Enigma rotors to the positions specified by the letters of his created key. In theory, this extra procedure would serve as an extra precaution for the Enigma’s security as a code breaker would have less material for making comparisons between messages of the same key. That is, if every message of a given day was encrypted with the same key, determining the set of alphabet substitutions used to decrypt the messages would merely require collecting enough different intercepted messages for comparing differences in the substitution behavior. The flaw which Rejewski was able to exploit was that the message key was ordered to be encrypted at the head of a message two times to avoid the error of decrypting a message with the wrong message key. So if an operator chose the letters A, J, and E for his message key he would have to type AJEAJE which, based on the given daily key, would be encrypted into a 6 letter clue indicating what the initial settings were. This clue was essentially the relationship between the first-third, second-fifth, and third-sixth letters as they were known to be the same.
Rejewski applied this observation to the large influx of encrypted messages intercepted each day and deduced that even though the letters used for the message key were arbitrary and unknown, the daily key’s letter-to-letter mapping had certain unique characteristics. For example with the three encrypted message keys KFGTCW, WPYOKH, and OSNGUK, Rejewski would observe that G maps to W, W maps to O, and O maps back to G. This produces a cycle of G-W-O-G. With enough intercepted messages of the same daily key, Rejewski would be able to find all existent cycles for a given day. Furthermore, it was determined that the length and number of cycles for a given day was unique and hence a signature of the rotor alignment portion of the daily key (Singh, 2000)7. This discovery was literally just the spark that the allies needed as the Polish proved that finding the daily key was in fact achievable. Rejewski would go on to create catalogues of these letter-cycle signatures which would be used as references for looking up rotor position portions of the daily key.
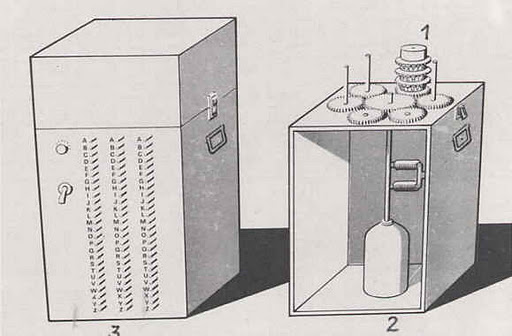
Even though Enigma messages could now be decrypted (which was still unknown by the German military), constant advancements in the Enigma’s security meant the need for constant advancements and reinvention on the part of the Polish cryptanalysts. During this period however, the Poles managed to create some very creative machines to aid in the process of calculating the Enigma’s setup of the day—two of which should be noted. The first was the Cyclometer which connected two sets of three rotors and copies of their respective reflectors in a closed electrical circuit (Kozaczuk, 1984)8. The positions of the rotors within the Cyclometer were arranged to represent the state of the Enigma machine before and after an arbitrary message key was produced, which meant the first rotor of one set was displaced by 3/26th of a full rotation. The electrical path which flowed through the arrangement of these rotors would produce the characters existent in the unique letter-cycle pattern created by a simulated daily key and display them on a glowlamp interface. By cycling through all possible configurations of the rotors, the cycle lengths corresponding to each respective rotor setup could be observed and catalogued. The second, more lasting innovation by the Polish cryptographers was the Bomb (or Bomba) which performed a similar operation to the Cyclometer but also accounted for the six possible arrangements of the three rotors within the Enigma machine. This required as many as six rotor sets to be configured in series through an electrical circuit so more possibilities of the daily key could be tested simultaneously. According to Rejewski, the bomb was able to do the work equivalent to 100 workers at the cipher bureau. (Kozaczuk, 1984)9
Eventually by 1939, it was the combination of introducing two new different rotors for potential use within the machine and the expansion of more plugboard wire usage which had finally exhausted the limits of Polish resources. With a new total of five possible rotors to choose from in determining daily keys, Polish technologies like the Bomb would require ten times the amount of rotor configurations connected in series to achieve the same results. The German military simply had more capacity to produce the same technologies which the Polish needed to keep up. This event was very untimely for Poland as it was clear by mid-1939 along with the rescinding of the Poland-Germany nonaggression pact, that an invasion was indeed imminent. Poland’s only option was to share their intelligence with Britain and France before it was too late.
Annotations and References
1. Singh, S., (2000). The Code Book: The science of secrecy from ancient Egypt to quantum cryptography. US: Random House Inc.
Chapter 3 of Singh’s The Code Book mentions the German enquiry into potential new encryption innovations. Singh also elaborates on the initiatives which sparked Germany to rethink their communication methods such as the accounts of their allied defeaters.
2. Rejewski, M. (1981). How the Polish Mathematicians Broke the Enigma. Annals of the History of Computing. 3(3), 213-34.
This first-hand account was originally published after Marian Rejewski’s death in a Polish periodical and it is one of Rejewski’s more technical accounts of the processes that went on at Biuro Szyfrow. One who is interested in the mathematical approaches involved in discovering portions of the daily cipher key should refer to this article as Rejewski lists slightly simplified examples of some of the problems he and his colleagues faced.
3,4. Kozaczuk, W., (1984). ENIGMA: How the German Machine Cipher was Broken, and how it was Read by the Allies in World War Two. Warsaw: Ksiazka i Wiedza.
“A Conversation with Marian Rejewski” is literally the translated recorded conversation between Rejewski and Richard Woytak, and is possibly his last recorded conversation. There is much discussed in this account, ranging from Rejewski’s dilemmas in career choices, to his experience within the cipher bureau. This can be found at Appendix B of Kozaczuk’s book.
5,6. Stengers, J., (2004). Enigma, the French, the Poles and the British 1931 -1940. Revue belge de philologie et d'histoire. Tome 82 fasc. 1-2. pp. 449-66
Though the depiction of Hans-Thilo Schmidt seems loosely caricatured in Stengers’s historical retelling (Singh’s The Code Book can be cross-referenced for a more accurate description), the contrary is true for the descriptive accounts of Captain Bertrand and his narrative on the French views of the Enigma cipher at the time.
7. Singh, The Code Book.
This is a simplification of the cyclic signature of the day keys. This is not to belittle the difficulty of Rejewski’s efforts. Singh provides a slightly, yet still simplified, description of this process.
8,9. Kozaczuk, ENIGMA.
Rejewski discusses the adversity faced by the ever increasing difficulties involving the changing machine ciphers. Found at Appendix E (The Mathematical Solution of the Enigma Cipher), there are a handful of processes and technologies that Rejewski attributes for calculating portions of the daily keys.
Cribs and Turing Bombes at Bletchley Park
As the fate of battling the Enigma changed hands from Polish intelligence to British intelligence, the rate of evolution on both sides of the communication battle only started to evolve more rapidly. Even with the founding of Bletchley Park, Britain’s new headquarters for code and cipher breaking which eventually housed up to seven-thousand workers, quicker methods for solving the Enigma’s daily keys was always an ever-pressing issue. And to make matters worse, the methods coined by Rejewski for determining the daily key, which heavily relied on the use of the doubly encrypted message key, saw the possibility of becoming obsolete.
It would be the famous mathematician and computer scientist Alan Turing, standing on the work laid down by Rejewski and the Polish, who would discover a weakness in the Enigma’s application so significant, that no German renovations to the standing machine would be able to prevent. At Bletchley Park, Turing was eventually given the task of exploring alternatives to Rejewski’s methods of finding the daily key, as British intelligence had the foresight to assume that the message key procedure, which revealed clues about the daily key, would not be around forever.
(Alan Turing)
During his study of the large compendium of messages accumulated by Bletchley Park, Turing was able to recognize adamant structures existing within the layout of German decrypted messages. These correspondences were so structured that Turing was able to begin predicting certain content of an intercepted message, based on the location and time it was transmitted as well as how it was structured. These predictions, often most effective when one word long, were labeled as “cribs” and provided the starting point for Turing’s research into bypassing the analyzation of the message key.
The observation of the cribs for purposes of decryption was very similar to the way Rejewski observed the inter-letter relationships of the message key. In fact, these ideas were so similar that Turing would eventually design his own Bombs (or Bombes) for processing key solutions based on cribs. This advancement in Allied cryptanalysis also required cleverness in other areas of the intelligence sector as well. Because the effectiveness of a crib depended solely on a certain piece ciphertext being correctly predicted, Allied intelligence would eventually try to coerce German transmitters into sending specific messages at predicted times. This often involved British forces broadcasting specific (sometimes fabricated) weather reports in hopes of finding the German word wetter in a designated location of an encrypted, yet structured weather report. A more effective measure taken by the Allies to get Germany to broadcast expected messages was the act of “Gardening,” or the laying of mines at sea in hopes that German U-Boats would discover and broadcast the mine coordinates which were already known by British intelligence and could thus be used as a potential crib (Singh, 2000)1.
It would eventually be this wounding blow to the Enigma’s security, along with strategic espionage and machine seizure, which would finally reach the seemingly impeccable U-Boat fleets. It is quite arguable that the Battle of the Atlantic would have taken a drastic turn, or at the very least significantly increased the length of the war, were it not for the great cryptanalytic minds that evolved alongside the technologies which dared them to evolve as well.
Annotations and References
1.Singh, S., (2000). The Code Book: The science of secrecy from ancient Egypt to quantum cryptography. US: Random House Inc.