The encryption war of WWII: the Enigma encryption machine: Difference between revisions
m (Added File Attachment Nonsimple wire diagram.gif -> Creation failed: Unsupported filetype!) |
No edit summary |
||
| Line 33: | Line 33: | ||
At this point in time, initial versions of the Enigma machine had already been built and had seen only failure in virtually all markets in Germany during the six years since its inception. Its inventor, Arthur Scherbius, had a keen interest in WWI cryptography—and more specifically—modifying the paper-and-pencil methods of the 19th century to utilize 20th century mechanized technology. Though the Enigma eventually underwent many modifications after its adoption by the German military, its remarkable design was founded on the ideas of Scherbius and improvements to the cipher failures of the past through mechanization. | At this point in time, initial versions of the Enigma machine had already been built and had seen only failure in virtually all markets in Germany during the six years since its inception. Its inventor, Arthur Scherbius, had a keen interest in WWI cryptography—and more specifically—modifying the paper-and-pencil methods of the 19th century to utilize 20th century mechanized technology. Though the Enigma eventually underwent many modifications after its adoption by the German military, its remarkable design was founded on the ideas of Scherbius and improvements to the cipher failures of the past through mechanization. | ||
[[Image: | [[Image:Nonsimple_wire_diagram.gif|510x357px]]<br> | ||
Scherbius’s design for the encryption procedure of the Enigma consisted of three independent components. A keyboard produced electrical signals which would pass as inputs through one of 26 different wires (A-Z) through the first component known as the plugboard or Steckerbrett. The plugboard acted as a redirector of input and output from the rest of the machine and consisted of an array of 26 dual-pass sockets, each representing a character of the alphabet. If a plug was connected into one socket, say ‘F’ for example, and the other end of the cable was inserted into the socket for ‘L’, a signal passing through one of the wires designated for either ‘F’ or ‘L’ would switch to its respective other upon passing through the plugboard. This component served as a simple substitution function for various input and could support up to 13 cables inserted in any way into the 26 sockets. Signals passing through the plugboard then come in contact with the next enciphering component—the rotor system.<br> | Scherbius’s design for the encryption procedure of the Enigma consisted of three independent components. A keyboard produced electrical signals which would pass as inputs through one of 26 different wires (A-Z) through the first component known as the plugboard or Steckerbrett. The plugboard acted as a redirector of input and output from the rest of the machine and consisted of an array of 26 dual-pass sockets, each representing a character of the alphabet. If a plug was connected into one socket, say ‘F’ for example, and the other end of the cable was inserted into the socket for ‘L’, a signal passing through one of the wires designated for either ‘F’ or ‘L’ would switch to its respective other upon passing through the plugboard. This component served as a simple substitution function for various input and could support up to 13 cables inserted in any way into the 26 sockets. Signals passing through the plugboard then come in contact with the next enciphering component—the rotor system.<br> | ||
| Line 67: | Line 67: | ||
''3.Rabah, K.V.O., (2005). Implementation of One-Time Pad Cryptography.Information Technology Journal, 4(1) 87-95.'' | ''3.Rabah, K.V.O., (2005). Implementation of One-Time Pad Cryptography.Information Technology Journal, 4(1) 87-95.'' | ||
''Rabah discusses various methods for creating random and pseudorandom streams of keys. The pseudorandom methods discussed include mathematical algorithms, however these methods are deterministic and not truly random. The random generation used for the production of one-time pad tables relied on natural processes observed in quantum mechanical events.'' | ''Rabah discusses various methods for creating random and pseudorandom streams of keys. The pseudorandom methods discussed include mathematical algorithms, however these methods are deterministic and not truly random. The random generation used for the production of one-time pad tables relied on natural processes observed in quantum mechanical events.'' | ||
<br> <br>[[Media:Nonsimple_wire_diagram.gif|Nonsimple wire diagram.gif]] | |||
[[Category:Radio_communication]] | [[Category:Radio_communication]] | ||
Revision as of 10:09, 11 December 2011
Blog Please check out my blog:[1] for updates on my research and what to expect for things to come on the GHN article.
Brief Overview
I’m a student in the History of Computing class at San Jose State University ([2]). This is a work in progress that will turn into a final article by the end of the semester in December of 2011. I welcome your comments and advice.
I am developing a java simulation of one of the encryption machines used in World War II by the Nazi military--The Enigma. During my research and development, I have been learning a lot about the disciplined effort that was made toward creating this encryption system that was (presumably) unbreakable; but this task at hand calls for the mentioning of even greater events happening simultaneously. The efforts of the computer scientists at Bletchley Park unarguably changed the course of WWII, and using one of the first modern day concepts of the computer in history -- the Colossus.
Upon completion of my Enigma simulator, I want to apply what I have learned about the machine's construction and use in war time and apply it to the perspective of the allied forces. I intend to define how Bletchley Park scientists determined their decryption algorithms and more importantly draw a relationship to the magnitude of their efforts in both revolutionary thinking in the field of computers as well as respective technological growth.
By December I intend to have a working simulation of the Enigma encryption machine along with algorithms derived from computer scientists at the time that can be applied to the simulator for decryption. Like with any history article, I intend to provide a solid historical grounding in the events which incited these technologies.
"Necessity is the mother of invention."
Mechanizing Encryption
In 1923 the British Royal Navy produced their official historical account of World War I. In this account, along with Winston Churchill’s The World Crisis, also published during the same year, it was openly released for the first time that the Allies’ advantages over the Germans were largely due to the acquisition of German codebooks and the decryption efforts of the British and French intelligence Bureaus (Churchill, 2005)1. This is undoubtedly true in many respects, ranging from the outcomes of naval battles at sea to the ultimate fact that Allied intelligence reduced the scale and duration of the war as a whole. In fact, the advantages provided by successful allied intelligence played such a large role during the course of WWI that up until the release of these publications, it was considered by French and British entities alike that such information should be kept secret from Germany at all costs.
Back in early 1917, despite German actions to go forward with their policy on unrestricted submarine warfare, the United States would have continued to remain neutral were it not for Germany’s incriminating plans against the U.S. that were discovered by British intelligence. It was Germany’s Foreign Minister, Arthur Zimmerman and his encrypted message to Mexico City that would change America’s mind, and consequently change the course of the war.
However during this dramatic point, even after Germany recognized that their communications had been discovered, the encryption security of such communications was never brought to Germany’s attention. It was indeed the British cipher breakers who discovered Germany’s intentions first, having decoded the Zimmerman telegraph weeks after its interception, but it was of great importance to the Allies that Germany never find out that their encryption security had been compromised for fear that they might improve their methods. Instead, this achievement by Britain’s Cipher Bureau and Allied efforts was masked by a constructed news story indicating that the famous Zimmerman telegraph was actually stolen from Mexico City only after its presumably safe travel. Almost seven years later in 1923, upon Britain’s release of their code breaking victories, Germany realizes its confidence in communications security had been misplaced.
At this point in time, initial versions of the Enigma machine had already been built and had seen only failure in virtually all markets in Germany during the six years since its inception. Its inventor, Arthur Scherbius, had a keen interest in WWI cryptography—and more specifically—modifying the paper-and-pencil methods of the 19th century to utilize 20th century mechanized technology. Though the Enigma eventually underwent many modifications after its adoption by the German military, its remarkable design was founded on the ideas of Scherbius and improvements to the cipher failures of the past through mechanization.
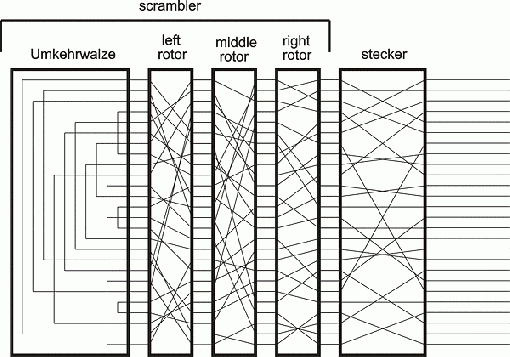
Scherbius’s design for the encryption procedure of the Enigma consisted of three independent components. A keyboard produced electrical signals which would pass as inputs through one of 26 different wires (A-Z) through the first component known as the plugboard or Steckerbrett. The plugboard acted as a redirector of input and output from the rest of the machine and consisted of an array of 26 dual-pass sockets, each representing a character of the alphabet. If a plug was connected into one socket, say ‘F’ for example, and the other end of the cable was inserted into the socket for ‘L’, a signal passing through one of the wires designated for either ‘F’ or ‘L’ would switch to its respective other upon passing through the plugboard. This component served as a simple substitution function for various input and could support up to 13 cables inserted in any way into the 26 sockets. Signals passing through the plugboard then come in contact with the next enciphering component—the rotor system.
A rotor by itself is responsible for another letter-to-letter substitution. Twenty-six electrical contacts on one face of the disk connect through internal wiring to 26 other contacts on the other side in a seemingly random relationship, changing the course of the input signal’s path through the machine. Scherbius’s design utilized three of these rotors, all with different internal wiring relationships, connected in series to provide three layers of substitution before exiting as output. However, arguably the most interesting thing about the Enigma machine is that these rotors would independently rotate at certain stages of enciphering a message so the cipher would constantly cycle through sets of substitution alphabets. How many substitution alphabets were possible as a result of this rotor series mechanism? Every time input is sent from the keyboard, the rightmost rotor in the machine would “step” by 1/26th of a rotation, essentially changing connections of each input lead of the rotor to the next output lead from the plugboard, and changing connections of each output lead of the rotor to the next input lead of its neighboring rotor. By the time the rightmost rotor makes a full rotation (26 keystrokes from the keyboard) the neighboring rotor to the left will be triggered to step once. So even though the rotor on the right has returned to its original substitution alphabet (orientation of its internal wiring relative to its input), the middle rotor has changed its orientation and so the substitution which spans both rotors is still completely different; and as the middle rotor comes to a full rotation, this consequently triggers a step in the left most rotor. To put this in perspective, an operator of the Enigma would have to depress 26*26*26 = 17,576 keys to arrive back at the original substitution alphabet that the machine started at, roughly more than six pages filled with encrypted letters.
The occurrence of a rotor step (other than the right most rotor which steps after every keystroke) is a result of the rotational orientation of the rotor to its right. This is caused by a detachable component of the rotor that could be referred to as the ring. The rotor’s ring—which is essentially a metal ring which fits around the outside edge of the rotor—has letter engravings around its circumference corresponding to the 26 internal wirings attached to each set of electrical leads. At a designated letter on each ring was a “notch” which when oriented in a certain position within the Enigma would trigger a neighboring rotor to step. The significance of the detachable property of this ring is that its notch (and the letter engravings corresponding to each wire connection of the rotor) could be adjusted, adding yet another variable element to the enciphering behavior of the machine.
Another ingenious property of these rotors is their compatibility with the Enigma in any arrangement. Any of the rotors labeled I, II, and III could be inserted into any of the three rotor slots; and because these three rotors were all different from each other in terms of internal wiring, each arrangement created a completely new set of substitution alphabets. Imagine now that the Enigma operator is encoding the same letter ‘A’ over and over. As outlined above, this would create a pattern that wouldn’t repeat itself until enciphering 17,576 ‘A’s, and furthermore this 17,576 letter long pattern would be completely different under any other arrangement of the three rotors.
During the post-WWI era, as exemplified by the events of the Zimmerman telegram decryption, cryptographers were constantly losing ground to cipher breakers and cryptanalysts. Creating strong enough ciphers was simply too inefficient, especially in the context of wartime, as they required very large sets of randomly generated substitution alphabets. Thus, achieving as many different cipher possibilities as what was now capable with the Enigma was extremely rare, but not impossible. In fact, it was the Americans during the end of WWI who gave birth to the idea that if a unique, randomly generated substitution alphabet was used for each letter in a ciphertext, decryption of such a ciphertext would be theoretically impossible if the cipher key was kept out of the hands of a code breaker. Without repeating the way a plaintext letter was mapped to its respective ciphertext, such an algorithm is virtually patternless and thus mathematically proven to be unbreakable without knowledge of what substitutions comprised the cipher.
However, this groundbreaking method came with its drawbacks. Before the use of Enigma-like machines for producing substitution alphabets, cryptographers using this system had to rely on large tables filled with hundreds of randomly generated letters. A long string of these letters with length equal to that of the plaintext to be encrypted would be taken from a given table and would serve as the basis for the polyalphabetic substitution. U.S. Army cryptographer Major Joseph Mauborgne coined this idea with the creation of the one-time pad which was essentially a thick stack of sheets with such randomly generated tables printed on them (Singh, 2000)2. If such a pad was produced and distributed to those responsible for sending and receiving encrypted messages, a key for decryption would never have to be exchanged. Instead, the only information that a cryptographer would have to include along with an enciphered message would be the starting position of the string of letters found on the first sheet of the one-time pad that a message receivers could refer to on their own one-time pad table. Such extra information would be useless to an outside interceptor without access to the random table that was used to produce the message, and because each sheet was intended to be discarded after use (hence the name “one-time pad”), the possibility of recognizing patterns in an encrypted message was nonexistent.
Even though the one-time pad offered this seemingly impeccable communication security, the cost and impracticality of creating such pads hindered their usefulness in many different contexts. For example in the heat of a war, if a one-time pad was seized by an enemy interested in decrypting messages, virtually all identical pads produced at the same time would be rendered useless because the message key could then be determined by those with access to the table of letters that were used. Such valuable references obviously could not afford to be on the battlefront. Furthermore, the production of these pads was neither timely nor cost-effective because the procedures for producing truly random sequences of letters (virtually free of any pattern) requires the reliance on processes found in nature, not human design (Rabah, 2005)3.
Scherbius’s rotor design offered a timely compromise to the drawbacks of the one-time pad by mechanizing the selection of alphabet substitutions. The Enigma produces an encryption cipher in the same fashion as the one-time pad process because each encrypted letter of a cipher text is produced by a unique and different orientation of the rotors’ internal wiring, with no repeated pattern as long as the message does not exceed 17,576 characters. Like the starting position on a one-time pad table, the initial setup of the Enigma’s rotors (along with the plugboard configuration) determines the entire cipher key for a translated message. This eliminated the need for mass-producing costly random letter tables and mitigated the vulnerability of decrypted messages in the event of a stolen Enigma. A captor of a machine would not be able to decrypt any given message without the additional knowledge of how the machine that produced such messages was initially set up. Having a machine provide the algorithm for encryption also increased the convenience for the cryptographer. Although heavy, the Enigma could be used in the most pressing of situations, creating messages on the fly and with some reductions to human error.
Decryption was just as convenient. One of the modifications to Scherbius’s design was an unchanging rotor-like component called a reflector, installed at the receiving end of the leftmost rotor. Although this component did not change states like the rotors did through stepping, it provided an additional substitution layer and something much more convenient. The reflector’s internal wiring would receive the signal produced by the leftmost rotor and would send the signal back through another terminal of the same rotor, reversing the path of the input. By doing this, an input was not only doubly-encrypted by the rotor mechanism, but the unchanging characteristic of the reflector ensured that inputs and outputs through the Enigma were reciprocals of each other. That is, if an Enigma at an arbitrary initial setup mapped the letter ‘A’ to the cipher letter ‘B’, another Enigma starting at the same setup would produce the cipher letter ‘A’ from the letter ‘B’. This allowed almost anyone with granted knowledge of the initial setup of the producing machine to decrypt ciphertext simply by sending each character through their own machine; operators responsible for sending top-secret messages no longer had to be as qualified or knowledgeable of cryptographic characteristics.
Like with any compromise however, these characteristics of the Enigma also provided security drawbacks. These draw backs will be discussed in later sections. One thing that should be noted about this transition to a mechanized way of encryption is the effect it had on many aspects of cryptology’s counterpart—cryptanalysis. Just as the achievements of the allied code breakers of WWI incited the Germans to bolster their communications security, significant advancements in encryption technology forced likewise evolution in the field of conquering these encryption secrets. This is not a unique theme as the ever-nascent battle between code makers and code breakers has existed since the dawn of information sharing, and the dramatic information battle of WWII is one of history’s great examples of this phenomenon.
Annotations and references 1.Churchill, W., (2005). The World Ciris. UK: Simon and Schuster.
Churchill lists many wartime events in which Naval procedures and counter-operations were incited from obtaining intelligence: codebooks, radio/telegraph interception.
2.Singh, S., (2000). The Code Book: The science of secrecy from ancient Egypt to quantum cryptography. US: Random House Inc.
The use of the one-time pad and the tables of randomly generated letter tables was mostly used in producing cipher keys for encrypting messages through the Vigenere cipher, a form of polyalphabetic substitution which relied on a string of characters as a basis for its substitution set. Although Major Mauborgne was not the originator of the randomly generated character set, the one-time pad innovation was largely credited to his introduction in WWI.
3.Rabah, K.V.O., (2005). Implementation of One-Time Pad Cryptography.Information Technology Journal, 4(1) 87-95.
Rabah discusses various methods for creating random and pseudorandom streams of keys. The pseudorandom methods discussed include mathematical algorithms, however these methods are deterministic and not truly random. The random generation used for the production of one-time pad tables relied on natural processes observed in quantum mechanical events.