History of Broadband Impedance Matching
History of Broadband Impedance Matching
This history of broadband impedance matching is organized chronologically by the birth date of each major design technique. Conceptual descriptions are for readers at the BSEE level, and mathematical symbolism and equations are minimal.
The bits and pieces of matching technology are scattered over the past 70 years. There are some substantially different developments that nevertheless fit together in important ways. Some separate techniques are also crucial to several others, especially optimization or nonlinear programming. Three books and an article have been made available on this IEEE Global History Network as downloadable PDF files to simplify reference retrieval (click on citations in blue type). More than 60 references are cited.
The Broadband Matching Problem
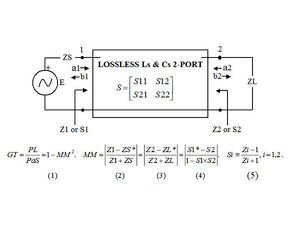
A crucial task in transmitter, amplifier, receiver, antenna and other RF applications is design of an impedance matching equalizer network as shown in Figure 1. The goal is to transfer power from source to load by transforming complex load impedance ZL=RL+jXL to match a resistive or complex source impedance ZS=RS+jXS over a wide frequency band. These impedances are usually measured at a finite number of radio frequencies. Sinusoidal source voltage E at any particular frequency is applied to lossless equalizer input port 1 through ZS, which can provide the maximum-available source power PaS to the load ZL when input impedance Z1= R1+jX1 = ZS* = RS-jXS (conjugate of ZS) according to equations (1) and (2). Otherwise, there is some power mismatch MM², which is the per-unit power reflected by the equalizer. Power mismatch is also expressed as Return Loss: RL=-20Log(MM). The goal is to find an equalizer network that minimizes the mismatch, thus maximizing the transducer gain GT in (1). Conjugate matching is not physically possible over a finite frequency band (Carlin and Civalleri, 1998:180). Note that reference page numbers may follow the citation year.
As in Figure 1, real power absorbed by load impedance ZL is the same power entering a lossless passive network, namely |a1|² − |b1|² = |b2|² − |a2|², which is the difference between PaS and reflected power. At a given frequency the generalized reflection coefficients in (2) and (3) are also equal in magnitude to the hyperbolic distance metric in (4) associated with impedances Z1 and Z2 through ordinary reflection coefficients S1 and S2 in (5). Hyperbolic distance between points on reflection charts is described in Section 3. According to good practice, impedances are generally normalized to 1 ohm and frequency to 1 radian/second (r/s). Reflection coefficients S1 and S2 in (5) differ from (2) and (3) only in that the latter have reactance XS or XL added to X1 or X2, respectively. According to a 1947 book sponsored by the US National Defense Research Committee:
”The techniques for matching a microwave device over a broad band are not well defined, and no practical general procedure has been developed for ‘broadbanding’ a piece of microwave equipment.” (Montgomery et. al., 1947:203).
That changed the following year (Fano, 1948) and has been evolving ever since. Most matching network research is based on lossless lumped L and C components, but there is a well-known frequency transformation that adapts those results to commensurate microwave transmission-line components (Richards, 1948).
It is crucial to recognize four different network termination arrangements: The preceding outlines the most general broadband double match case, as in Figure 1, where both load and source impedances are complex. The simpler broadband single match case involves a complex load and a resistive source, i.e. XS=0. Filter networks are either doubly terminated with only resistances RL and RS terminating or singly terminated with ZL=RL and ZS=0. In the latter case, either an ideal voltage or current source may provide the excitation. Filter design research flourished in the 1930s and was well understood by 1950 (Green, 1954).
Forerunner Technology 1939 -
Two tools crucial to broadband matching were described in 1939 and have been relevant ever since. Darlington’s Theorem says that an impedance function of an arbitrary assemblage of reactive and resistive elements can be represented by a reactive (lossless L and C) network terminated in a 1-ohm resistance (Darlington, 1939). Applied to Figure 1, for ZL=1+j0 there is always an LC network that can produce any impedance function Z1(p) versus complex frequency p = a+jw that is rational positive real. A positive real impedance function Z1 has R1>0 when a>0 and X1=0 when w=0. Positive real impedance functions occur as the ratio of specific polynomials in the complex frequency variable p. Darlington’s Theorem is evidently false if the 1-ohm termination is replaced by any other impedance, and that poses the compatible impedances problem (Youla et. al., 1997).
The Smith chart, initially conceived in 1939 for transmission-line analysis, is a transformation of all impedances in the right-half Argand plane (RHP) into a unit circle (Smith, 1939). That bilinear transformation was originally just as in equation (5) with the Smith chart center Zi=1+j0 ohms, but is equally applicable to (2) or (3) where the chart center corresponds to ZS* or ZL*, respectively. The Smith chart is utilized in Graphical Matching Methods in Section 7, and the related hyperbolic distance concept is crucial to the H-infinity technique in Section 9. The hyperbolic distance between Smith chart reflection point S1* and S2 according to equation (4) was described in 1956:
“The transformation through a lossless junction [two-port network] ... leaves invariant the hyperbolic distance ... . The hyperbolic distance to the origin of the [Smith] chart is the mismatch, i.e., the standing-wave ratio expressed in decibels: it may be evaluated by means of the proper graduation on the radial arm of the Smith chart. For two arbitrary points, W1, W2, the hyperbolic distance between them may be interpreted as the mismatch that results from the load W2 seen through a lossless network that matches W1 to the input waveguide.” (Westman, 1956:652,1050).
That curved distance metric on a Smith chart (geodesic) also can be expressed by the voltage standing-wave ratio (VSWR), which is a scaled version of the hyperbolic distance or mismatch as opposed to the original transmission-line voltage interpretation (Allen and Schwartz, 2001).
Analytic broadband matching theory was born in 1945 with a gain-bandwidth restriction on any single-match lossless infinite-element equalizer having a parallel RC load (Bode, 1945). This general limitation is a simple bound on the integral over all frequencies of mismatch (return) loss in decibels. For lowpass equalizers having an RC load, infinitely many elements, and a constant low reflection magnitude for frequencies below 1 r/s and unity above, the magnitude of S1 in (5) can be no less than e^(-Pi/RC). For corresponding bandpass equalizers, the minimum of the maximum constant mismatch is e^(-PiD) where the essential parameter is the decrement D=QBW/QL. QBW is the passband geometric-center frequency divided by the passband width, and QL is loaded QL=XL/RL at band center frequency (Cuthbert, 1983:193). This ideal result highlights the tradeoff between a good match over a narrow band and a poorer match over a wide band,
Finally, the broadband design techniques described in Sections 4, 5, 8, and 9 require complicated polynomial synthesis procedures. Regarding both theory and computation, a practicing synthesis expert noted:
"... the modern (insertion-loss) method of filter synthesis and design involves a very large amount of numerical computations, as well as, in most cases, the need to make choices that are anything but clear or simple. Furthermore, the numerical computations are nearly always very illconditioned, necessitating the use of either a large number of decimal places or esoteric procedures to overcome." (Szentirmai, 1997).
Analytic Gain Bandwidth Theory 1948 -
Analytic theory is required to understand gain bandwidth limitations; however, it can solve only simple RC or RLC single-match problems and requires those precise load models. Robert Fano extended Bode’s 1945 gain bandwidth theory for broadbanding the RC single match case by utilizing established doubly-terminated filter theory (Fano, 1950). The Fano technique replaces a qualified load impedance ZL (Figure 1) with Darlington’s resistively-terminated LC two-port network, so that what results is a doubly-terminated filter with resistors on both ends and two LC cascaded two-ports as the equalizer. The overall problem is to design a Chebyshev or elliptic equal-ripple doubly-terminated filter having a specified number of elements.
The poles and zeros of the given ZL impedance function rigidly fixed one of those two-port networks constituting the matching equalizer. Therefore, there was less flexibility to choose passband width, response shape, and tolerance (flat loss) while maintaining physical realizability of the LC two-port matching elements. This last requirement was satisfied by a set of Cauchy integral constraints similar to Bode’s primary result cited above, except that the upper bounds involve the LC elements in the load-equivalent Darlington network and the right-half p plane zeros of the input reflection coefficient S1. Fano solved only a few special cases with performance tradeoffs for certain types of RLC loads, but more general results were “hampered in most cases by mathematical difficulties which lead to laborious numerical and graphical computations.” (Fano, 1948:34)
Fano’s approach was soon made more simple and applicable, first by discovery of Chebyshev network element equations for the single- and double-match cases (Green, 1954) as later cited by others (Matthaei et. al., 1964:131). Less convenient continued-fraction expansion of Chebyshev polynomials for elements in single-match equalizers and singly- and doubly terminated filters also were reported (Matthaei, 1956), and extended to exclude transformers (Plotkin and Nahi, 1962). The Fano integral constraints were more simply tabulated and sloped passband responses for interstage networks were included to offset high-frequency gain rolloff in amplifiers (Mellor, 1975). Explicit design formulas for simple single-match broadband networks were published (Chen, 1976)
Fano’s analytic gain bandwidth theory was extended to include the double match case by adding a second Darlington network to represent a qualified source impedance ZS (Fielder, 1961), and optimal matching limits for that case were calculated by a simple iterative algorithm (Levy, 1964). Chen assembled design formulas for double-match broadband networks (Chen, 1988); for a list of articles in which the formulas first appeared, see (Gudipati and Chen, 1995:1647). A new theory employed scattering parameters with complex normalization, making Fano’s representation of the load impedance (by a Darlington equivalent LC network terminated in a one-ohm resistor) unnecessary. Equations (2) and (3) in Figure 1 were defined in that different approach, which formulated the matching constraints with Laurent series expansions (Youla, 1964:32). That complex scattering approach was applied to both single- and double-match equalizer design, and the concept of compatible impedances further extended that technique (Wohlers, 1965).
Applying gain bandwidth limits to simple lumped terminations motivated load and source modeling, which often required de-embedding diode or FET device circuit models from sampled measured data (Bauer and Penfield, 1974), (Medley and Allen, 1979). Late in the history of analytic gain bandwidth theory, it was shown that designing a Chebyshev equal-ripple passband for single matching is achievable but not optimal (Carlin and Amstutz, 1981). Furthermore, for the double-match case, selective flat gain to an arbitrary tolerance is never physically realizable (Carlin and Civalleri, 1985); the Real Frequency Techniques in Section 8 overcome that limitation.
Dissipative Equalizers 1953 –
Although lossy matching is not a popular technique, it is informative to know that a resistive, matched x-dB attenuator (pad) placed between a source and load reduces maximum available power by x dB, of course, but also reduces reflectance return loss by 2x dB (Westman, 1956:570).
Darlington briefly considered semi-uniform dissipation (all Ls have one unloaded Q value, Cs another) to synthesize lossy filters (Darlington, 1939), and subsequent consideration of broadband matching using those lossy equalizer elements extended Fano gain-bandwidth and Youla scattering parameter theories (LaRosa, 1953). LaRosa gave three reasons why lossy matching networks might be better than lossless ones: First, a lossless network might not be able to provide the desired low return loss over the passband: second, input return loss and power delivered to the load impedance are not independently controllable with a lossless matching network; and third, a dissipative network might have a simpler form than a lossless one.
Lossy equalizers without transformers were later considered (Gilbert, 1975), and selected lossy lumped networks were optimized to include sloped-gain passbands (Liu and Ku, 1984). Bode later elaborated on Darlington’s general theory, stating that any lossy or lossless network could be transformed to a lossless network if two element impedances are proportional, so that a rational impedance function exists (Zhu et. al., 1988).
However undesirable deliberate power loss may be, otherwise unmatchable narrowband antennas may force lossy matching to obtain a tradeoff between bandwidth and power efficiency (Allen and Arceo, 2006). A Pareto front is generated by an adaptive weighted-sum approach to multi-objective optimization problems with bounded random variable sets (Chu and Allstot, 2005). Using sets of random element values in a lossy matching network, one may plot a pattern of dots representing optimal results on a graph of input reflection coefficient magnitude (reflectance) versus system power loss. The boundary of that cluster nearest the origin is the two-dimensional Pareto front; it shows the best tradeoff between equalizer power reflected and power dissipated.
Developers of the H-infinity global optimal matching theory (Section 9) have also shown that a globally-optimal lossless matching network preceded by a resistive pad produces a Pareto front that is simply a negatively-sloped straight line segment in the linear graph of reflection coefficient versus system (pad+LC) power lost. Therefore, such a resistive pad sweeps out the best gain-reflectance tradeoff (Allen et. al., 2008b). Engineers may prefer an equivalent nonlinearly-scaled plot of VSWR versus system power loss in dB for various optimal LC network degrees and topologies. Also, the resistive pad may be replaced by dissipative network elements (Gilbert, 1975), and their sensitivities could be included to create a 3-D gain/reflectance/sensitivity Pareto front.
Numerical Optimization 1956 -
Optimization (nonlinear programming) is the technique for minimizing a nonlinear scalar function of many variables that may be constrained in various ways. In simple notation, the objective to be minimized is some scalar function f(x) subject to constraints c(x)≤0, where x is the vector of scalar variables and c(x) is a vector of scalar constraint functions. Optimization by varying parameters of candidate broadband matching networks has been a step in many major design techniques. Unfortunately, determining starting variable values and uncertainty of the search finding a global (deepest) minimum are two major weaknesses inherent in numerical optimization.
Joseph Louis Lagrange defined the calculus of mathematical optimization involving only equality constraints in 1804, but numerical applications depend on digital computers and a scientific programming language. That started with the IBM Model 650 computer in 1954 and the programming FORTRAN II formula translation language accommodating complex data in 1958. The easily treated least squares objective function was an early choice for circuit design (Aaron, 1956). The first truly effective unconstrained numerical optimization algorithm (Fletcher and Powell, 1963) was also applied sequentially in a straightforward algorithm for enforcing nonlinear constraints by the Lagrange multiplier method (Powell, 1969). The PET and Apple personal computers with the BASICA language made numerical optimization available to every engineer in 1977.
First partial derivatives of the optimization objective function with respect to each of the NV variables are required for rapidly convergent descent algorithms, e.g., Fletcher-Powell. Finite-difference perturbation of each variable for approximating first partial derivatives lacks accuracy and requires NV+1 simulations of network response at each of NS frequency samples, usually NS>2NV, so finite-differencing increases computing time on the order of NV^2. An amazing result in 1969 based on adjoint networks and Tellegen’s Theorem showed that all NV exact first partial derivatives could be obtained with only two network simulations per frequency (Director and Rohrer, 1969). This was a crucial development for optimization search schemes, which are highly iterative. Even so, exact first-partial derivatives for ladder network topologies can be obtained with even less computation (Orchard, 1985:1092). Also, the matrix of second partial derivatives can be estimated from the vector of first partial derivatives by using Gauss-Newton searches that save significant computing time (Nocedal and Wright, 1999:259).
Network optimization soon followed availability of digital computing and Fortran programming (Calahan, 1968:181-244). Choice of optimization variables distinguished the several approaches, including matching desired coefficients in rational polynomials in complex frequency p = a+jw, varying polynomial pole and zero locations in the p plane, and varying the L and C values in candidate matching networks. The last technique was later found to be less illconditioned by many orders of magnitude and thus more accurate (Orchard, 1985:1089). It is advantageous to transform the element values to logarithmic space to concentrate variables about unity (Iobst and Zaki, 1982:2168), and also derivatives of the objective function are thus normalized by their respective variable values, i.e. Bode sensitivities (Cuthbert, 1987:381).
For good conditioning of the objective function, it has long been known that the input reflection coefficient in equation (2) is a bilinear function of each L and C in a network (Penfield et. al., 1970:99), so varying any single network element traces an image circle tangent to the interior of the input unit reflection Smith chart. The corresponding mismatch over the passband, which is the distance from chart center to points on the input image circle, is a well behaved, unimodal curve between zero and unity and is ideal for numerical optimization for both single- and double-match problems (Cuthbert, 1999:137).
Statistical optimization methods increased in popularity with computer speed and are most relevant for multi-objective optimization problems. Genetic search and simulated annealing search methods are computationally expensive and not very effective for weighted-sum cost functions. However, an effective comprehensive statistical optimizer has been implemented to display tradeoff and design alternatives along a Pareto front followed by a Monte Carlo sensitivity analysis (Chu and Allstot, 2005).
Graphical Methods 1961 -
The bilinear function in equation (5) maps the impedance RHP into a unit circle, the Smith chart, which originally displayed lines of constant R and X (Smith, 1939). Besides widespread applications for designing impedance matching at a single frequency, many engineers became adept at recognizing chart impedance loci over frequency bands to design elementary broadband matching networks (Jasik, 1961). The Carter chart is the same bilinear mapping but show lines of constant impedance magnitude and Q (Q=X/R). The Q parameter indicates the relative energy stored in the tuning-element impedance; thus, greater Q implies less passband width. An unsophisticated broadband impedance matching design is based on Carter charts with impedance element transitions selected to keep each element loaded Q minimized (Glover, 2005).
Real Frequency Techniques 1977 -
The analytic gain bandwidth technique in Section 4 is based on a load model that characterizes the equalizer termination(s) by a prescribed rational transfer function with pole and zero singularities in the complex frequency p = a+jw plane. The real frequency technique (RFT) was a new and different approach based on load characterization by samples in real frequency only on the p = jw axis so that no load model was required (Carlin, 1977). Load impedance ZL (Figure 1) is sampled at no less than 2N frequencies, where N is the assumed degree of the equalizer. Back impedance Z2= R2+jX2 is determined by employing an approximately optimal R2(w) function over all real frequencies in the Hilbert transform integral to determine X2 and thus Z2. Darlington’s theorem then assures a single-match equalizer.
The first step in Carlin’s RFT is a piecewise linear functional guess of R2 over the entire w axis with the variables being the increase in R2 over each linear segment, i.e. excursions (Cuthbert, 1983:219). Then the least-squared mismatch MM in Figure 1 equation (3) is minimized over those variable excursions using sampled ZL impedances, piecewise R2 estimates, and X2 related by the Hilbert integral. With that optimal sampled R2, a nonnegative, even rational function of R2(w) is obtained by a second optimization that varies both numerator and denominator coefficients. Then a standard Gewertz procedure (Cuthbert, 1983:58) converts the rational R2(w) resistance function to a rational Z2(w) LC impedance function, from which a Darlington synthesis final step realizes equalizer element values. A concise algorithm for both the single- and double-match cases was published later (Carlin and Yarman, 1983:20-23). The MATCHNET PC DOS program for single- and double-match RFT synthesis of both lumped and commensurate transmission-line equalizers was published still later (Sussman-Fort, 1994).
A different RFT approach obtains the Z2(w) function in Figure 1 directly in a form guaranteed to represent a physical lowpass or bandpass double-match equalizer (Yarman and Fettweis, 1990). The parametric representation of Z2(w) by Brune functions is a form of partial fraction expansion with numerator residues that are functions of the (LHP) pole frequencies in their respective denominators. The transducer power gain (1) is maximized by varying the positive-real and imaginary parts of the N complex pole frequencies to calculate Z2 for use in (3). Thus, the laborious Gewertz procedure is not required and numerical stability is improved. Synthesis of the equalizer element values is still required, but the Brune functional form allows an efficient zero-shifting long-division algorithm. An intelligent guess of the initial variables is required, and the Brune parametric method does not provide partial derivatives for the optimization algorithm.
A third RFT approach for obtaining a lowpass Z2(w) function in Figure 1 in the single-match case (XS=0) uses a bilinear transformation to map the entire real frequency axis onto a unit circle (a Wiener-Lee transform). Expanding Z2(w) in a Laurent series then models R2(w) and X2(w) as Fourier series with cosine and sine basis functions, respectively. Starting with an initial guess of R2(w) values, transducer power gain (1) is maximized over a passband using cosine coefficients as variables constrained to keep R2(w)>0 (Carlin and Civalleri, 1992). First and second partial derivatives are available for the optimization. A Darlington synthesis step is still required to realize equalizer element values. Use of frequency mapped to a unit circle and the Fourier transform appears similar to, but is not the same as, the technique in the next section.
H-Infinity and Hyperbolic Geometry 1981 -
An entirely different approach to both theoretical and numerical techniques of broadband single-match was defined as a minimum distance problem in the space of bounded, analytic functions, particularly passive networks characterized by scattering parameters (Helton, 1981). A set of load reflectance values measured at discrete real frequencies is converted to respective center and radius values of eccentric constant-gain circles as commonly plotted on a Smith chart in the design of amplifiers. A spline extends these data to functions over the entire unit frequency circle, and approximate Fourier coefficients are obtained by the Fast Fourier Transform (FFT) to create a trigonometric series on a unit circle. Truncated Toeplitz and Hankel infinite matrices are constructed with those Fourier coefficients to form a simple matrix equation. Its smallest eigenvalue is calculated as trial mismatch parameter MM (reflectance) is varied to find the transition from positive to nonpositive definite, the result being the minimum-possible mismatch for a physically realizable equalizer (Allen and Healy, 2003), (Schwartz et. al., 2003). An algorithm for determining the optimal equalizer back reflectance (scattering parameter s22) for use in Darlington synthesis also was described; however, its validity has been questioned (Carlin and Civalleri, 1992:497). The first implementation of Helton’s H-infinity approach came many years later (Schwartz and Allen, 2004) and provided a gain-bandwidth bound and the Darlington equivalent s22 scattering parameter, but not the matching equalizer.
H-infinity is the Hardy space of matrix-valued functions that are bounded in the RHP and where passive network scattering parameters are contained in the unit ball. Nehari’s Theorem is the computational workhorse in H-infinity theory; it explains how to find an analytic function in the Hardy space that is the best approximation of a given complex function defined on the unit circle (Allen and Healy, 2003:28). The Helton method defined the given function of frequency as constant gain circles in a Smith chart, and the metric for proximity to a physical network’s scattering parameters is the hyperbolic distance or mismatch, equation (4) in Figure 1. The result is the best possible performance bound by optimizing over all physical broadband-matching equalizers.
Mathematician and Helton advocate Allen published a comprehensive book that applied H-infinity theory to optimizing broadband matching, amplifier gain, noise figure, and stability, all of which are circle functions on a Smith chart (Allen, 2004). He states on page 201:
“Anytime we have presented the H-infinity results to any electrical engineers, their immediate question is always – Where is the matching circuit? The most conservative answer is that H-infinity theory does not supply a matching circuit – the H-infinity theory computes the best possible performance over all the lossless matching circuits. It is very rare in numerical optimization to know the global minimum. The H-infinity theory equips the amplifier designer with the best possible performance to benchmark to assess candidate matching circuits.”
“This leads to the solid engineering question: How complex should the 2-port be to get an acceptable match? One approach plots the mismatch as a function of degree d. As the degree d increases the mismatch approaches the upper bound computed by Nehari’s Theorem. ... Thus Nehari’s bound provides one benchmark for the matching 2-ports.” (Allen and Schwartz, 2001:31).
“In practice, often the circuit designer throws circuit after circuit at the problem and hopes for a lucky hit.” (Allen and Healy, 2003:4). “The H-infinity solutions compute the best possible performance bounds by optimizing over all possible matching circuits. The engineering approaches typically specify a matching circuit topology and optimize over the component values. The State-Space (SSIM) Method stands between these two extremes by optimizing over all possible matching circuits of a specified degree.” (Allen, 2004:xii).
“The main (SSIM) program sets up the parameters for MATLAB’s minimizer ‘fmincon.’ Each search starts by initializing the minimizer ... by uniformly randomly selecting Nrep elements ... and starting the search at that random point.” (Allen and Schwartz, 2008a).
Systematic Search 1985 –
A crude systematic grid search originated from sampling one variable along a line interval at equal subintervals, or two variables on sides of squares, or three variables on sides of cubes, etc., with the “curse of dimensionality” exponentially increasing computing time. One approach was based on design of a ladder impedance-matching networks by a grid search in the bounded space of loaded Q parameters involved in transforming impedance to admittance at a single frequency (Abrie, 1985:215-231). A frequency in the upper passband was selected for this “1 plus Q squared” algorithm to impedance match with less than some specified maximum mismatch (2). The set of Q values for each series or parallel ladder-network element ranged from about –4.6 to +4.6 with subintervals of 0.5 to 0.8. A least-squares optimizer then improved one or more equalizers from a small set of acceptable network topologies.
Another systematic approach was based on recursive least-squares (regression) identification from control system technology (Dedieu et. al., 1994). Ladder network equalizers found by a recursive stochastic identification equalization (RSE) algorithm were refined by a random search in the region. The topology of candidate ladder networks was assumed, and sensitivities (normalized first partial derivatives) of power gain with respect to each network element were computed by the adjoint network (Tellegen) method for use in a Gauss-Newton minimization algorithm. The flat loss in the power gain was adjusted manually. Many equalizers designed by this method resulted in a few elements converging to extreme values so that their removal did not affect power gain performance.
The GRid Approach to Broadband Impedance Matching (GRABIM) can accommodate a mix of lumped and distributed network elements and includes features of preceding algorithms with added advantage taken of bilinear element transformations and minimax optimization (Cuthbert, 2000). Twelve all-pole ladder network topologies composed of 2-10 Ls and Cs are candidates to single- or double-match tabulated impedance data at discrete passband frequencies. Because the reflection coefficient in (2) is a unique bilinear function of each network element (Penfield et. al., 1970:99), the mismatch loss at each passband frequency sample is a smooth unimodal curve versus the element value localized in element logarithmic space (0.1 to 10.0). This set of superposed curves presents a nonsmooth unimodal optimization objective. A grid search in element variable space approximately locates the potentially global minimum of the maximum mismatch at any passband frequency while avoiding transmission-line element periodicity anomalies. Then Powell’s Lagrange multiplier algorithm, in conjunction with a Gauss-Newton minimizer, precisely locates a minimax solution in this neighborhood, eliminating any superfluous candidate-network elements. No initial element values are required.
References
Aaron, M. R. (1956). The use of least squares in system design. IRE Trans. Circuit Theory, CT3, N4. Dec.: 224-231.
Abrie, P. L. D. (1985). The Design of Impedance-Matching Networks for Radio-Frequency and Microwave Amplifiers. Boston, MA: Artech House.
Allen, J. C. (2004). H-Infinity Engineering and Amplifier Optimization. Boston: Birkhauser.
Allen, J. C. and D. Arceo (2006). A Pareto approach to lossy matching. SPAWAR Systems Center San Diego TR-1942.
Allen, J. C. and D. F. Schwartz (2001). Best Wideband Impedance Matching Bounds for Lossless 2-ports. SSC San Diego T.R. 1859. (65 pages).
Allen, J. C. and D. F. Schwartz (2008a). Wideband matching circuit and method of effectuating same. US Patent 7376535.
Allen, J. C. and D. Healy (2003). Hyperbolic geometry, Nehari’s theorem, electric circuits, and analog signal processing. Modern Signal Processing, V.46, 1-62.
Allen, J. C., D. Arceo and P. Hansen (2008b). Optimal lossy matching by Pareto fronts. IEEE Trans. Circuits Sys. II, Express Briefs V55, N6.
June: 497-501.
Bauer, R. F. and P. Penfield (1974). De-embedding and unterminating. IEEE Trans. Microwave Theory Tech. March: 282-288.
Bode, H. W. (1945). Network Analysis And Feedback Amplifier Design. New York: Van Nostrand; Ch. 16.
Calahan, D. A. (1968). Computer-Aided Network Design, Preliminary Edition. NY: McGraw-Hill.
Carlin, H. J. (1977). A new approach to gain-bandwidth problems. IEEE Trans. Circuits Syst. April: 170-175.
Carlin, H. J. and B. S. Yarman (1983). The double matching problem: analytic and real frequency solutions. IEEE Circuits Sys., V30, N1.
Jan.: 15-28.
Carlin, H. J. and P. Amstutz (1981). On optimum broadband matching. IEEE Trans. Circuits Sys., V28. May: 401-405.
Carlin, H. J. and P. P. Civalleri (1985). On flat gain with frequency-dependent terminations. IEEE Trans. Circuits Sys., V32, N8. Aug.: 827-839.
Carlin, H. J. and P. P. Civalleri (1992). An algorithm for wideband matching using Wiener-Lee transforms. IEEE Trans. Circuits Sys., CAS39, N7. July: 497-505.
Carlin, H. J. and P. P. Civalleri (1998). Wideband Circuit Design. NY: CRC Press."
Chen, W. K. (1988). Broadband Matching: Theory and Implementations, 2nd Ed. NJ: World Scientific Publishing Co.
Chen, Wai-Kai (1976). Theory and Design of Broadband Matching Networks. NY: Pergamon Press.
Chu, M. and D. J. Allstot (2005). Elitist nondominated sorting genetic algorithm based on RF IC optimizer. IEEE Trans. Circuits Sys.,
CAS-I, Reg. Papers, V52, N3. Mar.: 535-545.
(Cuthbert, T. R. (1983). Circuit Design Using Personal Computers. NY: John Wiley. Also, Melbourne, FL: Krieger Publishing Co. (1994).
(Cuthbert, T. R. (1987). Optimization Using Personal Computers with Applications to Electrical Networks. NY: John Wiley.
(Cuthbert, T. R. (1999). Broadband Direct-Coupled and Matching RF Networks. Greenwood, AR.: TRCPEP Publications
(Cuthbert, T. R. (2000). A real frequency technique optimizing broadband equalizer elements. ISCAS 2000 - IEEE Intnl. Symp. Circuits Sys.,
May 28-31, 2000, Geneva, Switzerland: V-401 to V-404.
Darlington, S. (1939). Synthesis of reactance 4-poles. Jour. Math. Phys., Vol. XVIII. Sept. 275-353.
Dedieu, H.,. et. al. (1994). A new method for solving broadband matching problems. IEEE Trans. Circuits Sys., V41, N9.
September: Pages 561-571.
Director, S. W. and R. A. Rohrer (1969). The generalized adjoint network and network sensitivities. IRE Trans. Circuit Theory, CT16, 318-323.
Fano, R. M. (1948). Theoretical limitations on the broadband matching of arbitrary impedances. M.I.T. Tech. Report 41:
January, Res. Lab. Electron.
Fano, R. M. (1950). Theoretical limitations on the broadband matching of arbitrary impedances. J. Franklin Inst. Feb.:139-154.
Fielder, D. C. (1961). Broadband matching between load and source systems. IEEE Trans. Circuit Theory. June:148‑131.
Fletcher, R. and M. J. D. Powell (1963). A rapidly convergent descent method for minimization. Computer Journal, V28, 1067-1087.
Gilbert, E. N. (1975). Impedance matching with lossy components. IEEE Trans. Circuits Sys. CAS22, N2: Feb. 96-100.
Glover, I. Et. al. (2005). Microwave Devices, Circuits, and Subsystems for Communications Engineering. NY: Wiley, Section 3.9.3.
Green, E. (1954). Amplitude-Frequency Charisteristics of Ladder Networks. Chelmsford, Essex, England: Marconi House.
Gudipati, R. and W. K. Chen (1995). Explicit formulas for the design of broadband matching bandpass equalizers with Chebyshev response.
IEEE Intnl. Symp. Circuits Sys. 1995. May:1644-1647, V3.
Helton, J. W. (1981). Broadbanding: gain equalization directly from data, IEEE Trans. Circuits Sys., CAS28, Number 12, 1125–1137.
Iobst, K. W. and K. A. Zaki (1982). An optimization technique for lumped-distributed two ports, IEEE Trans. Microwave Theory Tech., V30, N12.
Dec.: 2167-2171.
Jasik, H. (1961). Antenna Engineering Handbook, 1st Ed. NY: McGraw-Hill: Section 31.7.
LaRosa, R. and H. J. Carlin (1953). A general theory of wideband matching with dissipative 4-poles. Polytechnic Inst Brooklyn.
NY: Defense Tech. Info. Cntr, AD0002980.
Levy, R. (1964). Explicit formulas for Chebyshev impedance-matching networks. Proceedings IEE. June: pages 1099-1106.
Liu, L. C. T. and W. H. Ku (1984). Computer-aided synthesis of lumped lossy matching networks for monolithic microwave integrated circuits
(MMIC's). IEEE Trans. Microwave Theory Tech., MTT32, N3. March 282-290.
Matthaei, G. L. (1956). Synthesis of Tchebycheff impedance-matching networks, filters, and interstages. IRE Trans. Circuit Theory, CT3.
Sept.: 163-177.
Matthaei, G. L., L. Young, and E. M. T. Jones (1964). Microwave Filters, Impedance Matching Networks, and Coupling Structures.
NY: McGraw-Hill. Also, Boston: Artech House (1980).
Medley, M. W. and J. L. Allen (1979). Broad-band GaAs FET amplifier design using negative-image device models.
IEEE Trans. Microwave Theory & Tech., V27, N9. Sept.: 784-788.
Mellor, D. J. (1975). Computer-Aided Synthesis of Matching Networks for Microwave Amplifiers. Stanford, CA: Stanford University
Thesis SEL-75-005.
Montgomery, C. G., R, H. Dicke, and E. M. Purcell (1947). Principles of Microwave Circuits, M.I.T. Radlab, Vol. 9.
Republished in 1964 by Boston Technical Publishers, Lexington, MA.
Nocedal, J. and S. J. Wright (1999). Numerical Optimization. NY: Springer-Verlag.
Orchard, H. J. (1985). Filter design by iterated analysis. IEEE Trans. Circuits Sys., V32, N11. Nov.: 1089-1096.
Penfield, P., R, Spence, and S. Duinker (1970). Tellegen's Theorem and Electrical Networks.
Cambridge, MA: M.I.T. Press, Research Monograph No. 58.
Plotkin, S. and N. E. Nahi (1962). On limitations of broadband impedance matching without transformers. IEEE Trans. Circuit Theory. June: 125-132.
Powell, M. J. D. (1969). A method for nonlinear constraints in optimization problems. Optimization (R. Fletcher, ed.). London, pp.283-297).
Richards, P. I. (1948). Resistor transmission-line circuits. Proc. IRE, V36, 217-220.
Schwartz, D. and J. Allen [2004] Wideband Impedance Matching: H∞ Performance Bounds, IEEE Trans. Circuits Sys.II: Express Briefs, 51(7), pages 364–368.
Schwartz, D. F., J. W. Helton, and J. C. Allen (2003). Predictor for optimal broadband impedance matching. U. S. Patent 6622092.
Smith, P. H. (1939). Transmission line calculator. Electronics, V12, N1. Jan. 29-31.
Sussman-Fort, S. E. (1994). Matchnet: Microwave Matching Network Synthesis Software and User's Manual, Automated Synthesis of Low-Pass, High-Pass, and Bandpass Lumped and Distributed Matching Networks. Boston, MA: Artech House.
Szentirmai, G. (1997). Computer-aided design methods in filter design: S/FILSYN and other packages, Chap. 3 in CRC Handbook of Electrical Filters, J. T. Taylor and Q.Huang, Eds. NY: CRC Press.
Westman, H. P. Editor (1956). Reference Data for Radio Engineers, Fourth Ed. NY: International Telephone and Telegraph Corp.
Wohlers, M. R. (1965). Complex normalization of scattering matrices and the problem of compatible impedances. IEEE Trans. Circuit Theory, CT12: 528-535.
Yarman, B. S. and A. Fettweiss (1990). Computer-aided double matching via parametric representation of Brune functions. IEEE Trans. Circuits Sys., V37, N2. Feb.: 212-222.
Youla, D. C. (1964). A new theory of broadband matching. IEEE Trans. Circuits Sys. CT11: 30-50.
Youla, D. C., F. Winter, and S. U. Pallai (1997). A new study of the problem of incompatible impedances. Intnl Jour. Circuit Thy. & Applis, V25: 541-560.
Zhu, L. et. al. (1988). Real frequency technique applied to synthesis of lumped broad-band matching networks with arbitrary nonuniform losses for MMIC's. IEEE Trans. Microwave Theory Tech., MTT36. N12. Dec.: 1614-1619.