Ancient Computers

Possible Future Research

Could the methods outlined here for using The Salamis Tablet be implemented electronically?

If so, are there computer technologies evolving that could use such an implementation?

Author's Forward

In Tokyo in 1964 I bought a Soroban with Kojima’s book "The Japanese Abacus: Its Use and Theory". An event that sparked my interest in abaci ... and in computers. After getting my M.Eng.(Elect.) at Cornell, my 30 year career included working on the design and construction of nuclear power plants, missile systems software engineering, and industrial and engineering computer systems sales and systems engineering. Deciding to become a high school math teacher at the end of 2000, I took a History of Math course as part of my M.Ed. Program at UMassLowell. I was struck by how easy it would be to use ancient Roman, Greek, Egyptian, and Babylonian numerals to record abaci calculation results. Prof. Gonzalez said, "Yes, but how would you do multiplication and division?" So as a hobby, I've worked the last 10 years to (re)discover the schematics and rules of the the Ancients used to do their accounting and engineering to support and empower the greatest empires in human history. I hope you find Ancient Computers interesting and useful, Steve Stephenson, M.Eng.(Elect.), M.Ed.
Math Teacher (precalculus and calculus)
Lowell High School, MA
http://sks23cu.net/MT/
July 15, 2010 (Retired 6/30/2013) P.S.: Before you edit Ancient Computers, please be sure you read and understand the whole article and the Works Cited, and have watched and understand all of Stephenson's videos. P.P.S.: Also available as of 7/15/2013 are paperback and eBook versions of Ancient Computers with essentially the same content (see Links). Because it's much easier to modify, updates will first show up on http://ethw.org/Ancient_Computers.

Introduction

If you stare at an old mechanical calculator it just sits there. It does no computing and is, therefore, not a computer. When a person starts punching the keys and turning the crank the person-device computes and is a computer. So too, an abacus is just an assembly of beads and rods or lines and pebbles, and is not a computer. But when a person uses the abacus to perform calculations, then the person-abacus is a computer. A remarkably fast and accurate computer, as demonstrated by a Japanese abacus (Soroban) operator who beat a skilled electric calculator operator in a contest in Tokyo on Nov 12, 1946 (Kojima-1, p.12).

In classic Greek architecture, an abacus is a flat slab of marble on top of a column’s capital, supporting the architrave, or beam. Such an abacus (perhaps chipped beyond use in construction) makes a fine flat surface on which to inscribe lines; from which we get the name, counting board abacus. Developed later, constrained bead devices with less arithmetic functionality are also called abaci, e.g., Roman Hand Abacus, Chinese Suan Pan, and Japanese Soroban.

The Ancient Romans were excellent practical engineers and architects. Even today we marvel over their accomplishments and wonder how they did them. For example, in a BBC2 sponsored series Building the Impossible, Episode 2: The Roman Catapult, structural engineer Chris Wise wonders how the Romans did the calculations necessary to design and build the Roman Catapult used to destroy the walls of Jerusalem, when the math necessary wouldn't be developed for 1500 years! (Watch 1st minute of http://youtu.be/q_dHpLAPM5I).

The Roman expression for 'to calculate' is 'calculus ponere' - literally, 'to place pebbles'. When a Roman wished to settle accounts with someone, he would use the expression 'vocare aliquem ad calculos' - 'to call them to the pebbles.' (Jen)

Certainly the Romans would also use their abaci for engineering calculations.

Historians have published conjectures for what ancient counting board abaci looked like and how they were used (Menninger, pp.295-306; Ifrah, pp.200-211). On p.205, Ifrah concludes, “Calculating on the abacus with counters was ... a protracted and difficult procedure, and its practitioners required long and laborious training.”

That is not true.

[top]

Clues

Clues for the true structure and methods of the ancient counting board abaci are contained in three extant artifacts: The Japanese Soroban (Kojima; Menninger, pp.307-310), The Roman Hand Abacus (Ifrah, p.210; Menninger, p.305), and The Salamis Tablet (Ifrah, p.201; Menninger, p.299).

Every rod on a Soroban represents one decimal digit (Figure 1). The bead above the bar represents five of the beads below the bar. Each bar can count from zero (no beads next to the bar) to nine (all beads moved next to the bar).

Figure 1: A Small Japanese Soroban

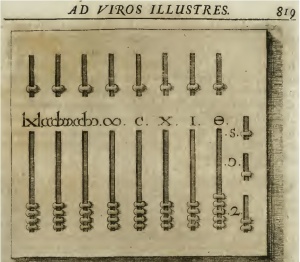
Figure 2A: Roman Hand Abacus Replica (Lütjens)	Figure 2B: Source for Figure 2A (Welser, p.819)

On the Roman Hand Abacus (Figure 2), each of the seven decimal digits has four beads in the lower slot and one bead in the upper slot; functioning exactly like the Soroban. It would be hard to understand why the Romans would not have developed similarly efficient methods to use the Hand Abacus as the Japanese did to use the Soroban (Kojima).

The two rightmost columns handle the Roman’s base-12 fractions and both count to twelve, but differently. The left column counts to five in the lower slot and carries into the upper slot on a six count, repeats to a count of eleven, then carries into the decimal units column on a twelve count. But the rightmost column breaks each six count into two three counts. Why the difference?

Mapping the Roman Hand Abacus slot symbols onto The Salamis Tablet of Figure 3 results in Figure 4.

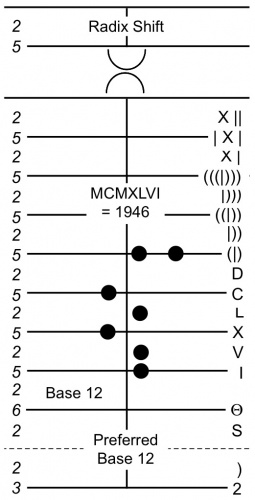
Figure 3: The Salamis Tablet before 300BC (Ifrah, p.201)	Figure 4: Roman Hand Abacus mapped onto The Salamis Tablet

The mapping is perfect. It uses the bottom grid’s eleven lines exactly, no more, no less. However, to do so the Romans had to use a less preferred structure for one of the base-12 digits. Why it’s less preferred is addressed below. But the fact that they had to make an engineering compromise is indicative that they used The Salamis Tablet as a design template for their Hand Abacus.

In Figure 4, the numbers on the left are the promotion factors that are dictated by the Roman Numerals mapped to the lines and spaces. For example, a promotion factor of 5 means that 5 pebbles on that line can be replaced by one pebble in the space above. All the spaces between lines have a promotion factor of 2. (The unused dashed line is explained below.)

Placing the Roman Numeral MCMXLVI = 1946 on the mapped Salamis Tablet demonstrates the use of the left side of the grid as a subtractive side. This is an extremely important observation as it reduces the number of pebbles needed tremendously, both in total and on each line or space. It makes the calculations much more efficient, robust, and rapid. An abacist would only need to carry a bag of pebbles that fits easily in a modern pants pocket to perform any of the four arithmetic calculations on any rational numbers with fewer than 11 decimal or 5 duodecimal (or sexagesimal) significant digits. (Stephenson, video 9.1)

As an example of using the subtractive side, if in the year 2009 = MMIX you wanted to calculate the age of a person born in 1946 = MCMXLVI, you would first make the 1946 in Figure 4 negative by moving each pebble to the opposite side of the vertical median line. (Follow along with pennies as pebbles and an abacus drawn on paper. Then to make room for the next addend, you would slide each of the pebbles as far away from the vertical median line as possible, left or right. Now you would add 2009 = MMIX by placing pebbles next to the median line: two on the right side of the (|) or M line, one to the left side of the I line, and one to the right side of the X line.

Merging the pebbles and replacing the C pebble with two L pebbles and one of the X pebbles with two V pebbles (both operations being demotions), then removing zero-sum pairs on every line and space (a pebble on each side of the median is a zero-sum pair) you read the answer LXIIV = 63.

While IIV is not considered by some people as a proper Roman Numeral expression, there are some rare examples of documents printed with both IIV and IIX type constructions (Handy). Proper form aside, these constructions do reduce the pebble count on counting board abaci, both in total and on each line and space. Using these constructions, any number can be registered with no more than two pebbles on any line or space.

Moving the pebbles of an accumulated sum away from the median as far as possible, there will always be room near the median to place another additive or subtractive number. Before combining the pebbles the abacist can check the addend for accurate pebble placement without damaging the accumulated sum. This checking, or auditing feature adds greatly to the accuracy and robustness of these methods. After checking, the pebbles are combined and moved to the outside ready for the next number to be added. Constrained bead abaci like the Suan Pan and Soroban cannot do this addend checking.

[top]

Roman Hand Abacus Design Compromise

The preferred base-12 digit configuration will never have more than two pebbles per line or space, but the other base-12 digit configuration will have three pebbles on a line for counts of 3 or 9. That is objectionable, both for pebble count per line or space as well as the psychological problem of handling two types of entities on the board. The more alike everything is, the faster and more accurately the operator can perform. The width of the counting board abacus would also have to be increased by 40% (14 vs. 10 pebble spaces per line).

In article 26 of The Aqueducts of Rome, Frontinus states, “… the inch ajutage, has a diameter of 1 1/3 digits. Its capacity is [slightly] more than 1 1/8 quinariae, i.e., 1 1/2 twelfths of a quinaria plus 3/288 plus 2/3 of 1/288 more.” Prof. Turner says that this value results from ( (1 1/3)² ) / ( (1 1/4)² ), where the squares are calculated before dividing.

The Romans would not have been able to do this calculation on the Roman Hand Abacus, nor on a Roman Hand Abacus mapped onto The Salamis Tablet. The number “1 1/2 twelfths plus 3/288 plus 2/3 of 1/288 more” written as a base-12 number is 1;1,7,10. That number has three base-12 fraction digits and you’d have to calculate a fourth for proper rounding. The Roman Hand Abacus only has two base-12 fraction digits.

So the Romans would have done the calculation on three coupled counting board abaci, each configured with 5 preferred-configuration base-12 digits, as in Figure 5.

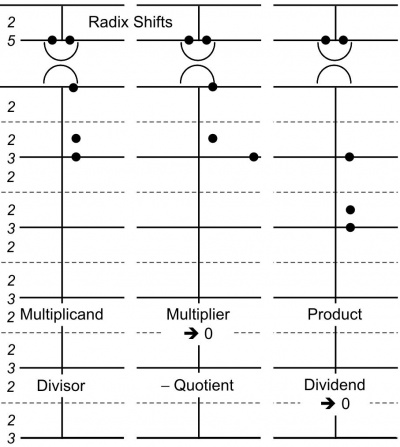
Figure 5. Three Base-12 Salamis Tablets Arranged for Multiplication or Division

The pebbles in Figure 5 are placed for the first step in squaring 1 1/3. The radix shift (what we call an exponent of 10) is shown as a zero-sum pair for both the Multiplicand and Multiplier to indicate no shift, so the unit line is the top line of the bottom grid.

Frontinus’ calculation, and others, are performed in a set of videos (Stephenson, videos 10.1-10.3, et al). It’s much easier and more insightful to watch someone doing the calculations than reading about how to do them. However, there are simplified tabular examples of Multiplication and Division in Appendix M.

[top]

Unused Dashed Lines

Why are the dashed lines unused? The Romans were borrowers. They borrowed The Salamis Tablet from the Greeks, but the Greeks borrowed it in turn from the Babylonians. The Babylonians used place value base-60 sexagesimal numbers written with reed styluses in cuneiform on clay tablets. Each of their digits contained 0-5 glyphs representing ten each and 0-9 glyphs representing one each, where there was at least one glyph; so each sexagesimal digit could represent the integers 1-59 (there was no zero symbol; see Figure 6).

Figure 6: Babylonian Numerals

To use The Salamis Tablet with base-60 numbers every sequence of line, space, dashed-line, and space, from bottom to top are assigned promotion factors of 5-2-3-2. Notice that in both the Roman duodecimal and Babylonian sexagesimal configurations the value of the space below any line is one half the value above. In essence, the Romans used a subset of the sexagesimal system for their duodecimal system.

The Babylonians also did not have a radix symbol (decimal point). But the context was always specified so the radix shift was always known and the base-60 number was, therefore, always a fraction less than 1 and greater than or equal to 1/60. So why would you need a radix symbol (or trailing zeros, for that matter)? This is evidence that the top grid on The Salamis Tablet is used for storage and manipulation of a radix shift, what we call an exponent of the base. Constrained bead abaci like the Suan Pan and Soroban do not have exponent capability.

So the Babylonians and perhaps the Sumerians had a computer using a place value number system and including the utility of near scientific notation as early as 2300 BC. Digital computers in use 4000 years ago!

But without a zero symbol, how could the Babylonians handle the one in twenty abacus results with empty digits (embedded zeros)? Two ways come to mind:

1. Convert to another unit of measure; e.g., 104 yards = 312 feet; or
2. State the answer in two parts; e.g., 104 yards = one hundred and four yards.

[top]

Plausible Historic Sequence of Abaci Development

1st abacus design

Your hands have 10 digits.

9834 with 24 pebbles:

  ––––––––––– 10000s

10–000000000– 1000s

10––00000000– 100s

10–––––––000– 10s

10X–––––0000– 1s

X marks unit line; promotion factors along the left; pebble values along the right.

[top]

2nd abacus design

Each hand has 5 digits, 2 make ten.

9834 with 16 pebbles:

 ––––––––––– 10000s
2         0  5000s
5––––––0000– 1000s
2         0  500s
5–––––––000– 100s
2            50s
5–––––––000– 10s
2            5s
5X–––––0000– 1s

[top]

3rd abacus design

Opposites, yin-yang, male-female, left-right.

Noting that 9=10-1=IX, 8=10-2=IIX, 4=5-1=IV, and 3=5-2,
9834 uses only 10 pebbles:

   –     +
 –––––|0–––– 10000s
2     |      5000s
5––––0|–0––– 1000s
2     |      500s
5–––00|––––– 100s
2     |0     50s
5–––00|––––– 10s
2     |0     5s
5––––0X––––– 1s

But since -100=(-50)+(-50) and -10=(-5)+(-5), [demotions]:

   –     +
 –––––|0–––– 10000s
2     |      5000s
5––––0|–0––– 1000s
2     |      500s
5––––0|––––– 100s
2   00|0     50s
5––––0|––––– 10s
2   00|0     5s
5––––0X––––– 1s

and since -k+k=0 [cancellation of zero pairs]:

   –     +
 –––––|0–––– 10000s
2     |      5000s
5–––––|––––– 1000s
2     |      500s
5––––0|––––– 100s
2    0|      50s
5––––0|––––– 10s
2    0|      5s
5––––0X––––– 1s

The value of 9834 can be represented with 6 pebbles.
(9834 = 10000 - 166)

[top]

4th abacus design

What if a number is larger than the abacus grid?
E.g., 9,834,000,000,000,000 = 0.9834 x 1016.

To the ancients the exponent would be a scaling number. They would enter 0.9834 at the top of the lower grid, then count how many lines down from the top the unit line should be, and enter that count in a new upper grid. The unit line on the bottom grid remains the top line.

Only 9 pebbles are needed to represent 9,834,000,000,000,000: 

   –     +
 –––––|––––– 100s 
2     |      50s 
5–––––|0–––– 10s 
2     |0     5s 
5–––––X0–––– 1s 
   Exponent

   Fraction
 –––––X0–––– 1s 
2     |      5/10s 
5–––––|––––– 1/10s 
2     |      5/100s 
5––––0|––––– 1/100s 
2    0|      5/1000s 
5––––0|––––– 1/1000s 
2    0|      5/10000s 
5––––0|––––– 1/10000s

[top]

5th abacus design

60 = 10 x 6 = 5 x 2 x 3 x 2, so the abacus design is easily extended to sexagesimal, and the Babylonians' cuneiform numbers fit nicely into the structure:

   –     +
 –––––|––––– 60s
2     |      30s
3- - -|- - - 10s
2     |      5s
5–––––X––––– 1s
   Exponent

   Fraction
 –––––X––––– 1s
2     |      3/6s
3- - -|- - - 1/6s
2     |      5/60s
5–––––|––––– 1/60s
2     |      3/360s
3- - -|- - - 1/360s
2     |      5/3600s
5–––––|––––– 1/3600s

[top]

Why Base-60?

But Why Base-60, 360 Degrees in a Circle, 7 Days in a Week, etc.? All from Sumer around 2500 BC (Wilson), and inherited by the Babylonians.

The Sumerians were great innovators in matters of time. It is to them, ultimately, that we owe not only the week but also the 60-minute hour. Such things came easily to people who based their maths not on a decimal system but on a sexagesimal one.

Why were these clever chaps, who went for 60 because it is divisible by 2, 3, 4, 5, 6, 10, 12, 15, 20 and 30, fascinated by stubbornly indivisible seven? ...

The Sumerians had a better reason for their septimalism. They worshiped seven gods whom they could see in the sky. Reverently, they named the days of their week for these seven heavenly bodies. (Wilson)

The divisibility of 60 was a convenient coincidental consequence, but not the primary reason the Sumerians adopted a sexagesimal number system . They did so from the periods of the two slowest moving of their seven sky gods. Jupiter and Saturn take 12 and 30 years, respectively, to track through the Zodiac. The observant Sumerians knew this. The least common multiple of 12 and 30 is 60.

In 60 years Jupiter would go through 5 cycles and Saturn 2. We have 5 fingers on each of 2 hands. In both cases 5+2=7, the number of sky gods. The mystical Sumerians would think of this as manifestations of the sky gods reflecting themselves in our anatomy.

The product of 12 and 30 is 360, the number of degrees in a circle; did the Sumerians define the 360 degree circle? Probably, because dividing the Zodiac into 360 degrees means Jupiter traverses 30 degrees in a year and Saturn 12 degrees; thereby coupling the periods of the gods Jupiter and Saturn.

The Sun tracks through the Zodiac in one year. Jupiter would track 1/12 of the way in that time. Why not divide a year into 12ths, i.e., 12 months; then the Sun tracks the same distance in one month that Jupiter tracks in one year; thereby coupling the periods of Jupiter and the Sun. And since the Sun would then track 30 degrees along the Zodiac in a month, why not divide the month into about 30 days, the period of Saturn? Then the Sun tracks about 1 degree every day. Of course the Sumerians knew that a year is actually 365 days simply by watching the sun track through the Zodiac, so maybe they just added a 5 day Holiday (like the Egyptians).

[top]

Designers of The Salamis Tablet

Both the astronomical and the anthropomorphic features of The Salamis Tablet in sexagesimal mode lead to the conclusion that the Babylonians, or their ancestors the Sumerians, were its designers; see Figure 7 (First scene of video 9.1, Stephenson). The Egyptians, Greeks, and Romans borrowed it for decimal and duodecimal calculations.

Figure 7: Structural Design of The Salamis Tablet

[top]

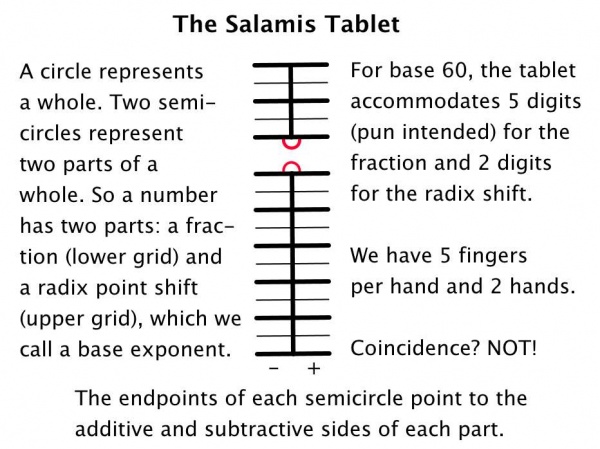
Computing in Sexagesimal

Assyriologists, using modern pen, paper, and computers to produce beautiful multifont typeset manuscripts, and using modern algebra and arithmetic as their basis for analysis, theorize that the Babylonians used tables of previously calculated values, recorded on clay tablets, to do their calculations.

For example, The MacTutor History of Mathematics' page, Overview of Babylonian Mathematics (retrieved 7/7/2005), states:

Perhaps the most amazing aspect of the Babylonian's calculating skills was their construction of tables to aid calculation. Two tablets ... give squares of the numbers up to 59 and cubes of the numbers up to 32. ... The Babylonians used the ... formula ab = [ (a + b)² - (a - b)² / 4 which shows that a table of squares is all that is necessary to multiply numbers, simply taking the difference of the two squares that were looked up in the table then taking a quarter of the answer.

To use this formula to multiply two five digit sexagesimal numbers proceed as follows:

(;a₁,a₂,a₃,a₄,a₅) (;b₁,b₂,b₃,b₄,b₅)

= (;a₁) (;b₁,b₂,b₃,b₄,b₅)
+ (;0,a₂) (;b₁,b₂,b₃,b₄,b₅)
+ (;0,0,a₃) (;b₁,b₂,b₃,b₄,b₅)
+ (;0,0,0,a₄) (;b₁,b₂,b₃,b₄,b₅)
+ (;0,0,0,0,a₅) (;b₁,b₂,b₃,b₄,b₅)

= (;a₁) (;b₁) + (;a₁) (;0,b₂) + (;a₁) (;0,0,b₃) + (;a₁) (;0,0,0,b₄) + (;a₁) (;0,0,0,0,b₅)
+ (;0,a₂) (;b₁) + (;0,a₂) (;0,b₂) + (;0,a₂) (;0,0,b₃) + (;0,a₂) (;0,0,0,b₄) + (;0,a₂) (;0,0,0,0,b₅)
+ (;0,0,a₃) (;b₁) + (;0,0,a₃) (;0,b₂) + (;0,0,a₃) (;0,0,b₃) + (;0,0,a₃) (;0,0,0,b₄) + (;0,0,a₃) (;0,0,0,0,b₅)
+ (;0,0,0,a₄) (;b₁) + (;0,0,0,a₄) (;0,b₂) + (;0,0,0,a₄) (;0,0,b₃) + (;0,0,0,a₄) (;0,0,0,b₄) + (;0,0,0,a₄) (;0,0,0,0,b₅)
+ (;0,0,0,0,a₅) (;b₁) + (;0,0,0,0,a₅) (;0,b₂) + (;0,0,0,0,a₅) (;0,0,b₃) + (;0,0,0,0,a₅) (;0,0,0,b₄) + (;0,0,0,0,a₅) (;0,0,0,0,b₅)

= (1;) [(;a₁) (;b₁)]
+ (;1) [(;a₁) (;b₂) + (;a₂) (;b₁)]
+ (;0,1) [(;a₁) (;b₃) + (;a₂) (;b₂) + (;a₃) (;b₁)]
+ (;0,0,1) [(;a₁) (;b₄) + (;a₂) (;b₃) + (;a₃) (;b₂) + (;a₄) (;b₁)]
+ (;0,0,0,1) [(;a₁) (;b₅) + (;a₂) (;b₄) + (;a₃) (;b₃) + (;a₄) (;b₂) + (;a₅) (;b₁)]
+ (;0,0,0,0,1) [(;a₂) (;b₅) + (;a₃) (;b₄) + (;a₄) (;b₃) + (;a₅) (;b₂)]
+ (;0,0,0,0,0,1) [(;a₃) (;b₅) + (;a₄) (;b₄) + (;a₅) (;b₃)]
+ (;0,0,0,0,0,0,1) [(;a₄) (;b₅) + (;a₅) (;b₄)]
+ (;0,0,0,0,0,0,0,1) [(;a₅) (;b₅)]

If only five significant figures are needed in the result, the terms in red can be discarded. Then there are nineteen products to calculate using the formula a_ib_j = [ ( a_i + b_j )² - ( a_i - b_j )² ] / 4. The result of a_i + b_j will be of the form (1;c_ij) half the time, in which case ( a_i + b_j )² = [ (1;) + (;c_ij) ]²  = (1;) + 2(;c_ij) + (;c_ij)².

On average, the calculation of each partial product would require: two additions, two table lookups, half a doubling, two subtractions, and two halvings. Combining the 19 partial products will require another 18 additions, being careful to add into the proper place value. In all, there are 56 additions, 38 table lookups, 8 doublings, 38 subtractions, and 38 halvings; a total of 178 operations!

How would you keep track of all this if you're limited to using reeds to write cuneiform on clay tablets? How many errors would you make? How would you find them?

Wouldn't it be simpler to suggest that the Babylonians developed and used abaci, with built-in error checking, to do their calculations?

[top]

YBC 7289 sqrt(2) Calculation

"The Babylonian clay tablet YBC 7289 (c. 1800-1600 BCE) gives an approximation of sqrt(2) in four sexagesimal figures" (retrieved 7/4/2010 from http://en.wikipedia.org/wiki/Square_root_of_2#History), a remarkably accurate achievement for the time.

The calculation of sqrt(2) on a set of sexagesimal Salamis Tablets using Heron's Method (see Figure 8) takes 25 minutes in Stephenson's videos 8.1-8.3.

Figure 8: Heron's Method.

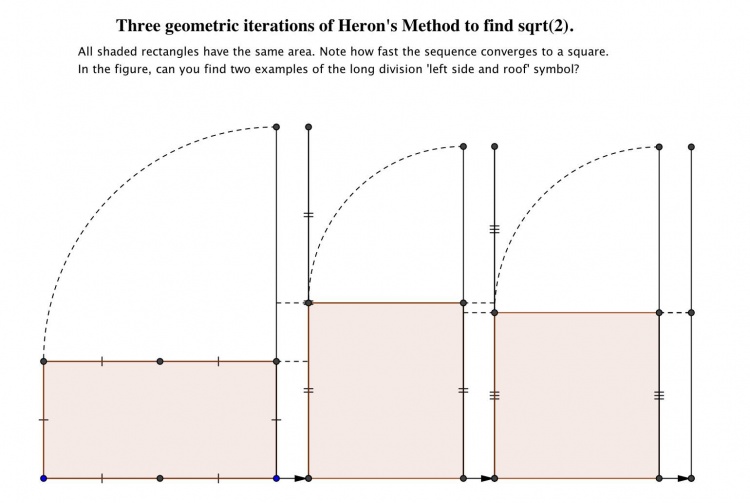
If Historians used the methods they think the Babylonians used (table lookups and such), and did it using just clay and reed styluses, they would probably take a lot longer than Stephenson's videos ... a LOT longer. The Historians should record their own video and post it to YouTube so we can compare its length to Stephenson's.

A possible analogy: in their early arithmetic practice exercises, modern elementary students learn how to perform long division and multiplication, and document the methods on paper. Then they are given four function electronic calculators and suddenly all their practice exercises document only the problem statement and the answer, with no work shown.

Just like the school tablets of the Old Babylonian period!

[top]

Conclusions

Features of the Roman Hand Abacus indicate that the Romans used a counting board abacus exactly like The Salamis Tablet for their heavy-duty calculations; it also gives us the promotion factors between lines and spaces. The Subtractive Notation of Roman Numerals indicates that one side of The Salamis Tablet grids are used for the additive part of a number and the other side for the subtractive part of the number.

The requirement of a four digit base-12 fractional answer to the calculation in article 26 of the book, The Aqueducts of Rome, indicates that the Romans used The Salamis Tablet in multiple configurations: decimal or duodecimal.

From these observations a consistent and powerful set of operational methods that the Romans must have used on The Salamis Tablet abacus has been identified.

The linkage between promotion factors of Roman duodecimal and Babylonian sexagesimal configurations, as well as astronomical and anthropomorphic features in the structure of the sexagesimal configuration, lead to the conclusion that the Babylonians, or their ancestors the Sumerians, were the designers of The Salamis Tablet and that they used much the same operational methods as the Romans, albeit with a different base. The Babylonians' lack of a radix point symbol suggests use of the upper grid of The Salamis Tablet to store and manipulate a radix point shift, or scaling factor; what we call an exponent of the base.

[top]

Notes

[top]

Works Cited

Frontinus, S. J. The Aqueducts of Rome. (B. Thayer, Producer, 2003, May 14) Retrieved June 21, 2010, from LacusCurtius: Into the Roman World: http://penelope.uchicago.edu/Thayer/E/Roman/Texts/Frontinus/De_Aquis/text*.html

Handy, C. (2000, August 15). Roman Numeral Year Dates: A Conversion Guide. Retrieved June 21, 2010, from http://www2.inetdirect.net/%7Echarta/Roman_numerals.html

Ifrah, G. (2000). The Universal History of Numbers. New York, New York, U.S.A.: John Wiley & Sons.

Jen, Dr. (1998, April 25). Roman Counting Instruments. Retrieved June 21, 2010, from The Math Forum at Drexel University: http://mathforum.org/library/drmath/view/57572.html

Kojima, T. Tokyo, Japan: Charles E. Tuttle Company.

1. (1954) The Japanese Abacus: Its Use and Theory.
2. (1963) Advanced Abacus: Japanese Theory and Practice.

Lütjens, J. (2010, April 5). Abacus-Online-Museum. (April 5, 2010) Retrieved June 21, 2010, from Jörn's Online Museum: http://www.joernluetjens.de/sammlungen/abakus/abakus-en.htm. Another web site,  http://www.tertisco-alexandru.com/abacus_project.html, cites the source of the image as Museo Nazionale Ramano at Piazzi delle Terme, Rome.

Melville, D. (1999, September 3). Old Babylonian mathematics. Retrieved July 6, 2010, from Mesopotamian Mathematics: http://it.stlawu.edu/%7Edmelvill/mesomath/obsummary.html

Menninger, K. (1969). Number Words and Number Symbols: A Cultural History of Numbers. (P. Broneer, Trans.) New York, New York, U.S.A.: Dover Publications.

Pullan, J.M. (1968). The History of the Abacus. New York, New York, U.S.A.: Frederick A. Praeger, Inc.

Smith, Glenn R. (2000, August 31). Retrieved July 12, 2010, from http://www.glenn.freehomepage.com/writings/articles.htm:

1. The Six Thousand Year Barrier
2. Phi, Pi and the Pentacle
3. The Sidereal Zodiac

Stephenson, S. K. (2009, August). How to use a Counting Board Abacus. Retrieved June 21, 2010, from http://www.youtube.com/view_play_list?p=545ABCC6BA8D6F44

Turner, J. H. (2007, December 19). Roman Elementary Mathematics: The Operations. (The Classical Journal, Vol. 47, No. 2 (Nov. 1951), 63‑74 and 106‑108) Retrieved June 21, 2010, from http://penelope.uchicago.edu/Thayer/E/Roman/Texts/secondary/journals/CJ/47/2/Roman_Elementary_Mathematics*.html#note4

Welser, M. (1682). Opera historica et philologica, sacra et profana. Referenced by Menninger on p.305 of his book, above. Retrieved June 21, 2010, from Open Library: http://openlibrary.org/books/OL23366519M/Opera_historica_et_philologica_sacra_et_profana.

Wilson, Andrew. the power of seven, The Classics Pages, The Economist, Dec 20, 2001. Retrieved July 4, 2010, from http://www.users.globalnet.co.uk/%7Eloxias/week.htm

[top]

Appendix C: Chinese Abacus

Citing Japanese scholars in the first chapter of his second book, Kojima explains that the Chinese DID NOT invent the Abacus.

They DID copy the Roman Hand Abacus after trading with the Romans over the Silk Road (http://en.wikipedia.org/wiki/Silk_Road).

Then they dismissed it, thinking it an inferior device, and ignored it for a thousand years, until the rise of business required faster arithmetic calculation speed than their numerals or home-grown devices were capable of.

[top]

Appendix M: Multiplication and Division Examples

In Multiplication a partial product for every Multiplier pebble on a solid line is added into the Product at the proper place value, and the Multiplier pebble is taken away. If there are no more Multiplier pebbles on solid lines (representing powers of the base) then a Multiplier pebble in a space is replaced by the equivalent number of pebbles on the line below, or the Multiplier is doubled and the Multiplicand halved, or vice versa. When there are no more Multiplier pebbles the product is complete. The radix shift of the Product is the sum of the Multiplicand and Multiplier radix shifts.

For example, to multiply the decimal numbers 0.84 and 0.93:

Step	Multiplicand	Remaining Multiplier	Incremental Partial Products	Accumulated Partial Product
0	0.84	0.93	0	0
1	0.84	1.00	0.84	0
		-0.10
		0.05
		-0.01
		-0.01
2	0.84	-0.10	-0.084	0.84
		0.05
		-0.01
		-0.01
3	0.84	0.05		0.756
		-0.01	-0.0084
		-0.01	-0.0084
4	0.42	0.10	0.042	0.7392
5	0.42			0.7812

In steps 1-4 the numbers in the Multiplier column are the values of individual pebbles. In step 4, instead of changing 0.05 to five 0.01s, the multiplier was doubled and the multiplicand was halved.

In Division appropriate additive or subtractive copies of partial products of the Divisor are combined with the Dividend until the remaining Dividend is zero, accumulating the partial product pebbles in the middle grid as the Negative of the Quotient. When the Dividend is zero, simply slide all the pebbles in the middle grid to the opposite side of the median and you have the Quotient. The Quotient’s radix shift will be the radix shift of the Dividend added to the opposite of the radix shift of the Divisor.

For example, to divide the decimal number 0.84 by 0.93:

Step	Divisor	Accumulated Neg. Quotient	Incremental Neg. Quotient	Dividend Increment	Remaining Dividend
0	0.93				0.84
1	0.93		-1.0	-0.93	0.84
2	0.93	-1.0	0.1	0.093	-0.09
3	0.93	-0.9	-0.001	-0.00093	0.003
			-0.001	-0.00093
			-0.001	-0.00093
4	0.93	-0.903	-0.0001	-0.000093	0.00021
			-0.0001	-0.000093
5	0.93	-0.9032	-0.00001	-0.0000093	0.000024
			-0.00001	-0.0000093
			-0.00001	-0.0000093
6	0.93	-0.90323	0.000001	0.00000093	-0.0000039
			0.000001	0.00000093
			0.000001	0.00000093
			0.000001	0.00000093
7	0.93	-0.903226	0.0000001	0.000000093	-0.00000018
			0.0000001	0.000000093
8	0.93	-0.9032258	-0.00000001	-0.0000000093	0.000000006
9	0.93	-0.90322581	0.000000001	0.00000000093	-0.0000000033
			0.000000001	0.00000000093
			0.000000001	0.00000000093
			0.000000001	0.00000000093
10	0.93	-0.903225806	-0.0000000001	-0.00000000009	0.00000000042
			-0.0000000001	-0.00000000009
			-0.0000000001	-0.00000000009
			-0.0000000001	-0.00000000009
11	0.93	-0.9032258064	-0.00000000001	-0.00000000001	0.00000000005
			-0.00000000001	-0.00000000001
			-0.00000000001	-0.00000000001
			-0.00000000001	-0.00000000001
			-0.00000000001	-0.00000000001
11	0.93	-0.90322580645			0.00000000000

So 0.84 / 0.93 = 0.9032258065. In the table, every number in the Incremental Neg. Quotient column represents one pebble.

For both multiplication and division there is no need for tables, printed or memorized, and the calculations are blindingly fast compared to any other methods available to the Ancients.

[top]

Appendix P: Pebble Efficiency

Assume two possibilities: using subtractive notation or not.

If you only have k pebbles, how high can you count sequentially on an 11 line abacus of the 3rd abacus design?

What patterns do the answers contain?

	Without Negative Parts		With Negative Parts
k	Maximum Sequential Count	Increment	Maximum Sequential Count	Increment
0	0	0	0	0
1	1	1	1	1
2	2	1	2	1
3	3	1	12	10
4	8	5	22	10
5	18	10	72	50
6	28	10	172	100
7	38	10	272	100
8	48	10	772	500
9	98	50	1,772	1,000
10	198	100	2,772	1,000
11	298	100	7,772	5,000
12	398	100	17,772	10,000
13	498	100	27,772	10,000
14	998	500	77,772	50,000
15	1,998	1,000	177,772	100,000
16	2,998	1,000	277,772	100,000
17	3,998	1,000	777,772	500,000
18	4,998	1,000	1,777,772	1,000,000
19	9,998	5,000	2,777,772	1,000,000
20	19,998	10,000	7,777,772	5,000,000
21	29,998	10,000	17,777,772	10,000,000
22	39,998	10,000	27,777,772	10,000,000
23	49,998	10,000	77,777,772	50,000,000
24	99,998	50,000	177,777,772	100,000,000
25	199,998	100,000	277,777,772	100,000,000
26	299,998	100,000	777,777,772	500,000,000
27	399,998	100,000	1,777,777,772	1,000,000,000
28	499,998	100,000	2,777,777,772	1,000,000,000
29	999,998	500,000	7,777,777,772	5,000,000,000
30	1,999,998	1,000,000	17,777,777,772	10,000,000,000
31	2,999,998	1,000,000	27,777,777,772	10,000,000,000

So using negative parts is 9,259 times more efficient than not using them. And there are those sevens again; yet another sign from their gods for the mystical Sumerians.

[top]

Appendix S: School Use Today

The Salamis Tablet abacus could be used in education to aid in the teaching of arithmetic, place value, exponents, and scientific notation.

On page 95, Pullan writes,

Much attention has been given to ways in which 'number concepts' develop in a child's mind, and one result of this has been the appearance of a variety of types of 'structural apparatus'. Properly used, they can undoubtedly be of great value, and many teachers have implicit trust in the particular type of apparatus they have chosen. There is, however, a fundamental objection to most of these devices. They give a different picture to each dimension, units, tens, hundreds, etc., whereas it is a basic principle of the Arabic system of notation that the same figures are used in each position. The naughts in such numbers as 10, 100, and 1000 are not intended to give a different appearance but to put the significant figure (in this case 1) in its proper place. They could be omitted if the position of the figure were known ... This difficulty does not arise on the abacus where the same counters 'sometimes stand for more, sometimes for less'; indeed, it is difficult to see what advantages the newly invented types of apparatus have over the old method of counter-casting.

Other positive features of using The Salamis Tablet in education include:

1. error checking an entry before accumulating, which is more forgiving for the young and/or novice (entering and accumulating are combined on constrained bead abaci, so if an error is made there is no indication and the error is propagated to the answer);
2. positive and negative numbers can be represented and manipulated simultaneously (without using complements as on constrained bead abaci);
   
3. the methods to accomplish all four arithmetic operations are much more transparent and straightforward than on constrained bead abaci;
4. numbers in near-scientific notation can be represented and manipulated (not possible on constrained bead abaci);
   
5. all four arithmetic operations, including multiplication as repeated addition and division as repeated subtraction, can be performed without memorizing tables;
6. advanced students can do all the above in base 10 decimal (Roman, Greek, Egyptian), base 12 duodecimal (Roman fractions), or base 60 sexagesimal (Babylonian) numbers (not possible on constrained bead abaci); and
7. much lower cost than either the apparatus discussed by Pullan or constrained bead abaci; i.e., for each abacus just draw some lines on paper and use less than 110 pennies as pebbles to perform all four arithmetic calculations on numbers of the form a × b^c where b = {10, 12, 60}, b^-1 ≤ a < 1, and 0 ≤ c < b^{2 (1+(b=10))}.

[top]