System of Measurement Units
Systems of Units
Nature of units
Engineering makes use of physical quantities in the broadest sense of that term, Le., including mechanical, chemical, physical, thermal and physiological quantities. In order adequately to compare the magnitudes of physical quantities of the same kind, unit magnitudes, or units, are necessary for each kind of physical quantity dealt with.
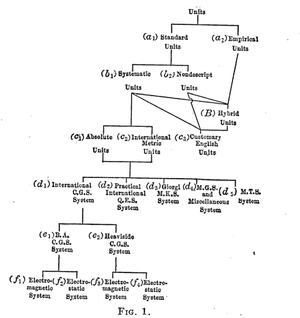
Classification of units.
(a1) Standard units may be said to include all units which have received the stamp of recognition in technical literature.
(a2) Empirical units, on the other hand, are units which have sprung into existence locally, ordinarily without any pretence to scientific derivation, and which have not been sanctioned by general usage. At various times during recorded history, empirical units have appeared. Thus. in the early history of electrical units, a unit of conductor resistance was used as representing the resistance of a certain length of a certain size of telegraph wire, as embodied in a certain standard resistance coil. Similarly, the average EMF of a Daniel cell was originally an empirical unit EMF.
(b1) Systematic units are units of any definitely related group. Thus the units "pint" "quart" "peck," and "bushel" entering into "dry measure are systematic units; because they stand in definite quantitative mutual relation as a group or system. Again, the units “mill”, “cent”, dime, and "dollar" entering Into American currency are systematic units.
(b2) Nondescript units may be defined as standard units which are not systematic or do not enter into any unit system. Thus, In Pennsylvania, a "bushel" of coarse salt, as a weight-unit is 80 lb. avoirdupois, * but in Illinois it is 50 lb. avoirdupois. *[World Almanac 1920, p84]
(B) Hybrid units, in contradiction to systematic units, are units which do not belong to any one system, but which are derived say from a plurality of different systems; from a systematic and a general unit; or from any combination of standard and empirical units. Thus, a “kilogram” may be defined as a unit of weight in the international metric system; while a “square foot” is a unit of area in the antique English system.
But the kilogram-per-square-foot," as a unit of weight loading of floor-area is a hybrid unit. Occasionally the advantage of practical convenience in the use of a hybrid unit may outweigh the disadvantage of its unsystematic derivation. No stigma necessarily attaches to the use of a hybrid, as distinguished from a systematic unit; but great caution has to be used in pursuing new and unfamiliar quantitative reasoning processes Involving hybrid units, lest numerical errors be introduced by neglect of coefficients.
(c1) Absolute units are units of physical quantities selected in a comprehensive scientific system based upon three or more. fundamental physical properties, such as length, mass, time, energy, specific gravity force, etc.; so that simple and fundamental quantitative relations may subsist between the members of the system and that each physical quantity may have one and only one unit in the system. The particular basic units from which a system of absolute units is derived are called the fundamental units of that system, while the units so derived are called the derived units in correlation thereto. In a dynamical system, the fundamental units are three only and are: a unit of length, a unit of mass, and a unit of time. Consequently, unless otherwise specified, the term" absolute units" is taken as referring to a scientific system based on fundamental units of length, mass, and time. But whereas only one set .of fundamental units has come into recognition-the length-mass-time set above mentioned-several species of this set have been used to some extent; namely, the “foot-grain-second” system, the “meter-kilogram-second" system, the "centimetergram-second" (C.G.S.) system, the "meter-ton-second" (M.T.S.) system. and the "quadrant-eleventh-gram-second" (Q.E.S.) system.
Only the last three have come into extensive practical use. The C.G.S. system has become the international scientific system, and the Q.E.S. system an international electromagnetic system in electrical engineering. Any complete electromagnetic absolute system involves five fundamental units, two of which may be constants of the ether.
(c2) Metric units are units pertaining to the international metric system. This system, which was created in France in 1792, was adopted in France in 1840, in Germany in 1872, in Austria in 1876 and so on from one civilized country to another; until at the present date. The only great communities which have not yet adopted the metric system are Great Britain, the United States and the Russian Empire (at 1923). The advantage of the system is its simplicity. It is a decimal system, using a single fundamental unit of length (the meter) and one of mass (the gram).
(c3) Customary English units are the units of the English and American measures, viz., length measure, square measure, land. measure, cubic measure, cord measure, dry measure, liquid measure, avoirdupois weight, tray weight, apothecaries weight and jewellers weight. Each of these measures may be regarded as a system. The complete list may be regarded as a congeries of imperfectly connected systems. Empirical and hybrid units are mingled with the rest.
(d1) C.G.S. units are the units of that particular system of absolute units which is based on the international centimeter, the international gram and the mean solar second. That is, they are absolute units employing the metric system in a definite way. A reason for the centimetre having been selected in place of the meter as the fundamental unit of length was that ,the mass of the cubic centimeter of water (at the temperature of unit density) is the gram or unit mass;- whereas the mass of a cubic meter of water would be a metric ton as in the M. T. S. system.
(d2) Q.E.S. units are units pertaining to the quadrant-eleventh-gramsecond absolute system; i.e., the system in which the unit of length is 109 cm. or 1 theoretical quadrant of the earth as measured from a pole to the equator the unit of mass is 10^-11 g. and the unit of time the mean solar second, or the 1/86,400th part of the annual mean daily period of revolution of the earth with respect to the sun. This is the system to which the international ohm, volt, ampere, joule, watt, coulomb, farad and henry, belong. The system was not intentionally established as a Q.E.S. system; but the ohm having been arbitrarily selected, for convenience of magnitude, as 10^9 C.G.S. electromagnetic units, and the volt similarly as 10^8 C.G.S. units, the rest of the system necessarily coincides with the Q.E.S. system; or is such a system as would be produced by the selection of the quadrant, eleventh-gram and second as fundamental units, together with unity for the permeability and unity for the dielectric constant of the ether.
(d3) Giorgi units are units in a combined absolute and practical system devised by Prof. G. Giorgi, [33] in which the fundamental units an,: the meterkilogram- second-international ohm, and the further assumption that the permeability of free ether, instead of being unity as in the C.G.S. magnetic system, is U0=4 PI. 10^-7 henry/m. On this basis the ohm-volt-ampere series of practical units become also absolute units. The electric inductivity, instead of being unity, as in the C.G.S. electric system, becomes ko = 1/36 PI X 10^-9 farad/m. No distinction arises in the Giorgi system between electric and magnetic units. The system is also rectified in regard to 4 PI factors, or is “rationalized" in the Heaviside sense; so that a number of fundamental equations in the system differ from those of the C.G.S. system III regard to such 4 PI factors.
(d4) M.G.S. units, etc. Units in an absolute system whose fundamental units are the meter-gram-second, the millimeter-milligram-second, the footgrain second, etc. None of these extraneous absolute systems have come into extensive use.
(d5) MTS System. Soviets and French briefly used a variant of the metric system where the base unit of mass was the tonne.
(e1) B.A. units are the units of the C.G.S. system as established by the British Association for the Advancement of Science in 1862. The electrostatic subsystem was established on the basis of the unit quantity of electricity such that it repelled its prototype at a distance of 1 cm. With a force of 1 dyne. The electromagnetic subsystem was similarly established on the basis of the unit magnetic pole such that it repelled its prototype at a distance of 1 cm. with a force of 1 dyne. This procedure led to the anomalous result that every electromagnetic quantity has a unit both in the electrostatic subsystem and in the magnetic subsystem.
(e2) Heaviside units are units in that form of the C.G.S. system which was first suggested by Mr. Oliver Heaviside in 1882. [22] He showed that if a unit electric point charge and a unit magnetic point pole had been respectively defined such that unit total flux emanated there from, the strength of the field at unit distance would be 1/(4 PI"),and this, not unity, should be the force in dynes that the prototype would develop in repulsion. As a consequence of this unnatural definition of the BA. unit charge and pole, the fundamental equations of the B.A. system become interlaced with 4 PI factors in rectilinear problems and denuded of them in spherical problems where they should naturally be expected to occur. Mr. Heaviside proposed to rectify the system by changing the fundamental definitions in the manner suggested, and enunciating a new list of units in both the electrostatic and magnetic subsystems; all related to the corresponding .B.A. units in Simple powers or roots of 4 PI. He similarly proposed rectifying the practical or Q.E.S. system of units by adopting a new ohm, volt, ampere, etc., all bearing some ratio of simple power or root of 4 PI" to the corresponding existing values. If Mr. Heaviside's proposals had been formulated and considered prior to international adoption of the ohm-volt-ampere series of units, and legalized standards, they might have been adopted. [28] At the present time a very few physicists employ Heaviside's “rational" units in theoretical analysis.
Fundamental principles concerning units in equations
Many of the equations representing propositions in pure 'mathematics maybe satisfied by quantities of any kind. Thus taking the very simple equation:
2(a+b) = 2a+2b
it is clear that the quantities a and b may be of the same kind or of different kinds, and their respective units may be any whatsoever, without affecting the identity expressed, so long as a and b have respectively the same meanings on the two sides of the equation.
When, however, as ordinarily in engineering, physical magnitudes are dealt with In an equation; then three consequences ensue; namely:
1. The equation can only be interpreted in terms of some unit of the particular physical quantity dealt with. This is the unit of the equation;
2. The unit employed on each side of the equation must be the same; and
3. If either side of the equation contains a simple sum of positive or negative terms; then each of these terms must employ the same unit as the equation.
This discipline is known as 'Dimensional Analysis'.
Historical Sketch of English Units
Weight
The English weights and measures are based upon old Roman weights and measures. * The troy pound is supposed to have been a weight of silver referred to as a "pound sterling." This pound would be coined into 240 silver pennies or "pennyweights," each of 24 gr. (barley grain weights).
It would, therefore, contain 5,760 gr. Heavy bodies (substances in gross outside of coins or bullion) were weighed by" avoirdupois" weight, authorized by law early in the fourteenth century. Several slightly different "avoirdupois pounds were in use. Since Queen Elizabeth’s reign the avoirdupois pound has been fixed at 7,000 troy grains.
Length
In regard to British lengths, the earliest seems to have been the cubit or half yard. The cubit is a very ancient measure, and corresponds to a forearm length from elbow to middle finger-tip. The royal iron standard yard was constructed in the thirteenth century, after which the cubit or half yard gradually fell out of use. The foot was standardized at one-third of the yard. The mile was a relic of the Roman “millia passuum" or thousand paces; the Roman pace was two of our paces, or counted between the lifts of one and the same foot.
Volume
Gallon measures of volume existed at different times in England in six different forms such as the corn-gallon, the ale-gallon, etc. Among these, the wine-gallon of Queen Anne contained 231 cu. in. This gallon was brought to America by the early colonists and remains today the US gallon. In 1824 the British enacted a new" imperial gallon" to supersede all pre-existing gallons, and defined it as the volume of 10 avoirdupois pounds of distilled water at the temperature of 62 deg. fahr. With the barometer at 30 in. It was further defined as a measure containing 277.274 cu. in. of distilled water. There is thus a difference between British and American gallons in the ratio 277.274 .to 231 = 1.204 : 1: so that the British gallons, quarts, and pints are respectively about 20 per cent. larger than American gallons, quarts and pints, a large discrepancy that has frequently led to major misunderstandings.
Area
In land measure, since Anglo-Saxon times, a “perch" or "pole " was 11 cubits in length = 16.5 ft., and such a pole was the surveyor's unit. A length of 40 perches was a furlong, and 8 furlongs the statute mile. An acre of land was the area of a rectangular strip a furlong in length and 4 perches in breadth, which breadth was known as the "acre's breadth”.
An acre therefore included 40 X4 = 160 sq. perches. Eight such strips end to end made the statute mile, and 80 such strips side by side made a statute mile breadth; so that a square statute mile contained 640 acres. Early in the seventeenth century, Prof. Edmund Gunter of Gresham College decimalized acre measure by inventing a 100-link “chain" of outstretched length equal to 4 perches or the acre's breadth (66 ft.). The acre thus became 10 sq. chains.
History of the International Metric System
Prior to 1790, differences existed between the weights. and measures of different Departments of France. Reform in the directions of simplification and unification was promised in a decree of the National Assembly under the sanction of Louis XVI in 1790. The metric system was actually developed under the authority of the French Republic in 1793, in the hands of a committee of scientists and engineers.
The decimal system, at the base of the metric system, was originally extended to angles and to time, the right angle being divided into 100 grades (centigrade), each subdivided into 100 minutes and again into 100 seconds. The day was divided into 10 hours, each subdivided into 100 minutes and again into 100 seconds. The decimal subdivision of time never came into extended effect, and the decimal subdivision of angles has only been used to a limited extent, except in France.
The meter was selected as a length equal to the ten millionth part of the northern quadrant of the earth, or distance from pole to equator at the meridian of Paris. Later measurements have shown that the international standard meter finally adopted is shorter than the 10-7 quadrant by 0.02 per cent. [38] The advantage of such a basis for the meter is that by the use of the decimal subdivision of angles: i.e., by the substitution of 100 grades for 90 deg, the kilometer becomes the natural nautical unit of distance, or the hundredth of the grade; just as the English nautical mile is the sixtieth of a degree.
The metric system is universally used in all European countries, except Great Britain and Russia. The quantitative literature of the scientific world is almost exclusively written in the metric system. To express quantitative relations exclusively in the English units is to conceal their meaning, to a great extent, from all but English-speaking peoples; and also to discredit them scientifically, by implication.
In the United States, the metric system has been a legally recognized system since July 28, 1866. In 1893, the U. S. Office of Standard Weights and Measures was authorized to derive the yard from the meter at the ratio 1 yd. = 3600/3937 meter. The customary weights are likewise referred to the kilogram. The customary weights and measures of the United States are thus defined in terms of, and maintained with reference to, the international metric system.
The international metric standards, i.e., the standard meter bar and the standard kilogram, are maintained at the International Bureau of Weights and Measures at Sevres, near Paris, France, in a building which has been declared internationally neutral or outside of French territory. Copies or prototypes of these standards are maintained at the various national laboratories and are occasionally intercompared.
Evolution of Electromagnetic System of Units
In 1861 a committee of the British Association for the Advancement of Science (B.A.) was appointed to consider standards of electrical resistance. The committee decided to adopt a series of electrical units in the C.G.S. absolute system. The unit of resistance in the C.G.S. magnetic system was so small (one-billionth of an ohm) that it was considered unfit for practical use and a unit 109 times greater than the C.G.S. unit was selected as of convenient magnitude. This decimally derived unit was called the ohm after the German scientist Dr. Ohm. Similarly, the C.G.S. magnetic unit of electromotive force was regarded as unfit for recommendation, and a unit 108 times greater than the C.G.S. unit was selected, and called the volt, after the Italian electrician Volta. The ohm having been selected as a unit, standard resistance coils had to be produced and adjusted-a work of great labor. In 1864 and 1865, certain standards of resistance or B.A. ohms were produced and put into service. In 1872, Mr. Latimer Clark produced the well-known zinc-mercury standard cell which bears his name.
B.A. ohm too small. In 1878, it was realized that the B.A. ohm was too small by over 1 per cent. That is, the B.A. ohm is now taken to be 0.9866 of the existing international ohm.
In 1881 an international electrical congress at Paris recommended that the standard ohm should be represented as the resistance of a uniform column of mercury, 1 sq. mm. in cross-section, at 0 deg. cent., the length of such a column for the B.A. ohm being approximately 104.9 cm. The Paris congress of 1881 also adopted the ampere, coulomb. and farad, as the practical units of• current, quantity and capacity. The practical system based on the ohm and volt thus became virtually the Q.E.S. (quadrant-eleventhgram-second) system, in place of the C.G.S. system; i.e., as though 10^9 cm. were substituted for 1cm as the unit length, and 10^-11 g. instead of 1 g. as the unit mass.
In 1882, an international commission met at Paris and adopted a length of 106 cm. as the length of the mercury column defining the ohm, as a closer approximation to the true ohm than the B.A. ohm. This 106-cm. ohm was called the "legal" ohm, as distinguished from the B.A. ohm. Legal ohms, volts, etc., have at the present date almost completely disappeared. They represented an intermediate stage of approximation to the present international unit values.
In 1889, an international electrical congress at Paris adopted the joule, the watt, and the quadrant, as the practical units of energy, power and inductance, respectively.
Edinburgh conference. In 1892, a conference was held in connection with the B.A. meeting at Edinburgh. It was then decided to adopt 106.3 cm. as the length of mercury column whose resistance should 'embody’ the ohm.
In 1893, the international electrical congress of Chicago adopted the 106.3-cm. ohm, which was called the international ohm. The other units of the practical system adjusted in conformity to this value were called correspondingly the international ampere, volt, coulomb, etc. The name of the unit of inductance was changed from the quadrant to the Henry, in honor of the American physicist of that name.
In 1900, an international electrical congress at Paris, after some debate, adopted the Maxwell as the unit. of magnetic flux and the Gauss as the unit either of magnetic intensity or of flux-density in the C.G.S. magnetic system.
In 1908, an international commission at London considered the order of sequence of resistance, current and voltage standards, which had been left indefinite at preceding congresses. It was decided that the ohm should be the first unit, and the ampere the second, as determined by the rate of electro-deposition of silver under specified conditions. The volt was to be determined from the ohm and ampere.
Definitions of Electric and Magnetic Units
Electric quantity (Q). The amount of electricity present in any electric charge or passed through a circuit during any time interval by an electric current. The practical unit is the coulomb, the C.G.S. units are the a coulomb and statcoulomb.
Electric e.m.f. or pressure (E). That which tends to make an electric current flow. E.m.f. is ordinarily accompanied by a difference of electropotential; but an e.m.f. may occur without difference of potential, as for example, when a straight bar magnet is thrust symmetrically into a circular loop of uniform wire. A brief current will thus be set up in the wire due to an e.m.f. induced by the magnet's motion; but there will be no difference of electric potential in or around the wire. The practical unit is the volt. The C.G.S. units are the abvolt and statvolt.
EMF may be reckoned for a complete circuit or for any portion thereof; that is, each and every portion of a closed circuit in the steady state obeys Ohm’s law.
Potential difference (U or V). A condition in virtue of which an electric current tends to flow from a place of higher to a place of lower potential. The numerical measure of the potential difference is the work done on a unit quantity of electricity in passing between the two points. The practical unit is the volt. The C.G.S. units are the abvolt and statvolt.
Potential gradient ( V/cm ). The space rate of change of potential, or the change with respect to distance. An electric potential gradient is the space rate ,of change of electric potential, and similarly for magnetic, thermal or gravitational potential. The systematic unit in the practical system is the volt per quadrant, but a hybrid Unit such as volt per centimeter is generally used. The C.G.S. unit is either the abvolt or statvolt per cm.
Electric current (I). The rate at which electricity flows through a conductor or Circuit. The practical unit is the ampere, which is a current of one coulomb per second. The C.G.S. unit is either the absampere or statampere.
Electric current density (I/sqcm). The ratio of the current flowing through a conductor to .the cross-sectional area of that conductor. More strictly, the current density at a point in a conductor is the ratio of the current through a very small plane element of section containing the point and perpendicular to the current, to the area of the element. The systematic practical unit is the ampere per square quadrant. In practice, a hybrid unit is preferred such .as the ampere per Square centimeter or square inch. The C.G.S. uni is either the absampere or statampere per square centimeter.
Electric resistance (R). Obstruction to electric flow. The ratio of voltage to current In a conductor or closed circuit. The practical unit is the ohm. The C.G.S. unit is either the absohm or statohm.
Electric resistivity (p). The ratio of potential gradient in a conductor to the current density thereby produced. Also the specific resistance of a substance numerically equal to the resistance offered by a unit cube of the substance as measured between a pair of opposed parallel faces. The system practical unit IS the ohm-quadrant or numerically equal to the resistance in a cubic earth-quadrant. A hybrid unit such as the ohm-cm. is usually preferred. The C.G.S. magnetic unit is the absohm-cm. See Resistivity.
Electric conductance (G). The conducting power of a conductor or Circuit for electricity. The inverse or reciprocal of electric resistance. The practical unit is the mho. The C.G.S. unit is either the abmho or the stamho.
Electric conductivity (gamma). The specific electric conducting power of a substance. The reciprocal of resistivity. The systematic practical unit is the mho per quadrant. A hybrid unit, such as the mho per cm. is usually preferred. The C.G.S. magnetic unit is the abmho per cm.
Inductance (L) The capacity for electromagnetic induction possessed oy an active circuit either on itself or on neighbouring circuits. The ratio of the magnetic flux linked with and due to an active conductor (number of turns X total flux) to the current strength carried. The practical unit is the henry. The C.G.S. units are the abhenry and stathenry.
The term Inductance seems to have been first introduced by Heaviside. [39] as a brief equivalent for “coefficient of self-induction." Inductance may be divided into two species; namely, self-inductance and mutual inductance. The unit is the same for both species.
Electric capacitance (C). Sometimes called permittance or capacity. The power of storing or holding an electric charge. The ratio of an electric charge on a conductor to the electric potential difference producing the charge. The practical unit is the farad. The C.G.S. unit is either the abfarad or the statfarad. The term "permittance" was introduced by Heaviside [40]. It should be noted that capacitance is used by a few writers as synonymous with capacity-reactance.
Permittivity is the specific permittance of a substance and numerically equal to the permittance offered by a unit cube of the material as measured between a pair of opposed parallel faces. In the C.G.S. electric system it is equal to k,. the dielectric constant. Analogous to electric conductivity and magnetic permeability, a term introduced and defined by Heaviside.
Dielectric constant or specific inductive Capacity (k). The ratio of the capacity of a condenser whose coatings are separated by a given substance, to the capacity of a similar condenser whose plates are separated by a vacuum. A pure numeric in any system of units.
Elastance. The reciprocal of the capacitance of a condenser or dielectric. No unit for elastance has been agreed upon in any system. The term "daraf" has, however, been suggested for this unit in the practical system, so that a condenser having a capacity of one farad would also have an elastance of one daraf. The C.G.S. unit would be a statdaraf.
Elastivity. The specific elastance of a substance, and numerically equal to the elastance offered by a unit cube of the substance as measured between a pair of opposed parallel faces. In the C.G.S. electric system it is the reciprocal of permittivity. Analogous to electric resistivity. No units.
Frequency (f). In a simple alternating-current circuit the number of cycles executed by the current per second. The unit is the cycle per second, or Hertz.
Angular velocity (w) of a simple alternating-current circuit. The product of the numeric 2 PI and the frequency f of the current in cycles Del' second. The unit employed is the radian per second.
Reactance (X). In a simple alternating-current circuit, the reactive component of the impedance, as distinguished from the active component, resistance. Reactance may be divided into two species of mutually opposite signs;" namely, inductive reactance or that species of reactance developed in an inductance, 2wfL, and condensive (capacitive) reactance, or that species of reactance developed in a condenser, ½ PIfc. Inductive reactance is denoted (when using the method of complex imaginary quantities) by the sign +j, and condensive (capacitive) reactance by the sign -j. The unit of reactance in the practical system is the ohm. The C.G.S. unit is either the absohm or statohm.
Impedance (Z). The apparent resistance of an alternating-current circuit or path. The vector sum of the resistance and reactance of the path. The practical unit is the ohm. The C.G.S. unit is either the absohm or statohm.
Admittance (Y). The reciprocal of the impedance of an alternating current circuit Or path, a complex quantity. Units mho, ablnho or statmho.
Conductance (G). In a direct-current circuit, the reciprocal of the resistance. The 'practical unit is the mho. In Germany it is called the Siemens. The C.G.S. unit is either the abmho or the statmho.
In a simple alternating-current circuit, the conductance is the active component of the admittance, or the quantity which multiplied by the root-mean-square impressed alternating voltage gives the active component of root-mean-square current, or the component in phase with the e.m.f. The practical unit is the mho. The C.G.S. unit may be either the abmho or statmho.
Susceptance (B). The reactive component of admittance in a simple alternating-current circuit. The practical unit is the mho. The C.G.S. unit may be either the abmho or statmho.
Magnetic poles. Those portions of the surface of a magnetic source where the magnetic flux enters or leaves the surface. Magnetic poles appear wherever there is an abrupt change of permeability.
Magnetic pole strength. The total flux entering or leaving a pole divided by 4 PI. No name has been provided for this unit. The product of magnetic pole strength and the length of the magnet (interpolar distance) is the magnetic moment.
Magnetic flux (Phi). The magnetic flow or current that passes through any magnetic circuit. The CGS magnetic unit is the Maxwell.
Magnetic flux-density (Beta). The ratio of the magnetic flux in any cross-sectional element of a magnetic circuit to the area of that element. The CGS magnetic unit is the gauss, which is also a maxwell per square centimetre.
Magnetomotive force (m.m.f.). That which produces magnetic flux. The analogue in the magnetic circuit of electromotive force in the electric circuit. No name has been provided for the unit of m.m.f either in the practical or in the C.G.S. magnetic system. The name of gilbert has, however, been suggested for the latter. A convenient practical unit is the ampere-turn which is 4 PI/10 = 1.25663705427 gilberts.
Magnetic field intensity (H) or gradient of magnetic potential, also termed magnetizing force. The rate of change of magnetic potential with respect to distance. In a region of unit permeability, the field intensity is numerically equal to the magnetic flux density, The provisional name of the C.G.S. magnetic unit is the gilbert per centimeter. A numerically related hybrid unit is the ampere-turn per centimeter.
Reluctance (R) Obstruction to magnetic flow. In a simple magnetic circuit, the ratio of the m.m.f. to the magnetic flux. A provisional name for the C.G.S. magnetic unit is the oersted. One gilbert m.m.f. acting on a magnetic circuit of one oersted reluctance produces one maxwell of flux.
Reluctivity (p). A specific reluctance, numerically equal to the reluctance of unit cube of a substance between any pair of opposed parallel faces. The C.G.S. magnetic unit is the oersted-cm.
Permeance. The reciprocal of reluctance. Conducting power for magnetic flux. No name has been adopted for this unit.
Permeability (mu). The reciprocal of reluctivity, or specific permeance. No name has been adopted for this unit. In the dimensional formulas of the C.G.S. system, if the electric and magnetic constants of the ether are considered as mere numerics; both permeability and reluctivity are also mere numerics. Also magnetic intensity has the same dimensions as flux density; [44] so that on this basis, which was at one time undisputed, there would be no difference between gilberts-per-centimeter and gausses except numerically. It is now generally admitted, [50] however, that the electric and magnetic constants of the ether should not be taken as mere numerics; although their dimensional formulas are not defined. On the latter basis, there is a dimensional difference of same kind between magnetic intensity in gilberts-per-centimeter and flux-density in gausses. The permeability can also be expressed as mu=1+4 PI K where K is the susceptibility.
Electrical resistivity. Resistivity may be defined quantitatively either in terms of "mass resistivity" (pm), or of "volume resistivity" pv. The defining equation of mass resistivity is R M gram ohms is:
(pm) = R/L . M/L gram.ohms/sq meter
It is the product of the linear resistance in ohms per meter and the linear mass in grams per meter. R is the resistance of the wire in ohms, M its mass in grams, and L its length in meters. A uniform copper wire of 100 per cent. conductivity 1 meter long, at 20 deg. cent., and weighing 1 gm. would have a resistance of 0.15328 international ohm. The defining equation of volume resistivity is:
pv=R.A/L = 1/§ (R/L . M/L) microhm-cm.
where R is the resistance of the wire in microhms, A is its uniform cross-sectional area in sq cm., L its length in cm. and § the density of the wire.
At 20 deg. cent., a wire of 100 percent conductivity,1 cm. long and of 1 sq. cm. in cross-section would have a resistance of 1.7241 microhms.
Since in accurate measurements of wire conductivity, the length, weight and resistance of the wire are always determined, the mass resistivity is more fundamental than the volume resistivity in engineering. Their ratio is the density § when the units employed are identical in both. The density of copper is taken as 8.90 gm. per cu. cm. at 0 deg. cent. and 8.89 at 20 deg cent., the temperature coefficient of linear expansion being 17 x 10^-6. Owing to the effects of expansion the temperature coefficients of the two resistivity’s are not identical.
Telephony Measurement Units
Moving forward a few years, here are some of the telephony system measurement units:
- dBm
= Absolute level of a signal in dB relative to 1.0mW
= 10 log ( level/0.001W)
= dBr + dbmO
- dBmO
= Absolute level of a signal (which would appear) at a point of zero relative level. This is a normalised level.
= dBrncO - 88.3
= -SNR
= 10 log (pWpO) - 87.5
= dbmOp + 2.5
= dBm - dBr
- dBr
= The 'design' level at a point in a transmission channel RELATIVE TO a point of 0 relative level. It is a label.
- 0dBr
= A point of zero relative level in a tramsmission channel. At this point the mean absolute signal power during the busy hour is -15dBm or 32uW.
- dBuVEMF ( a kirchoff voltage)
= dBuV + 6db
- dBrncO
= 88.3 + dBmO
= 90.8 +dBmOp
= 10 log [pWp0] + 6.8
= 88.3 - SNR
= dBa0 + 6.8
- dBa0
= 10 log [pWp0] - 6.0
= 84.0 +dBmOp
- SNR
= -dBm0
= -[dBm0p +2.5]
= 88.3 - dBrnc0
= 87.5 - 10 log pWp0
References
[22] Heaviside, O. “The Relations between Magnetic- Force and Electric Current." The Electrician, London: Nov. 18, 1882.
[28] Heaviside, O. "Electrical Papers." Macmillan Co., 1892, Vol. II, p. 575
[33] Ascoli, M. “On the Systems of Electrical Units," Trans. Int. Electrical Congress of St. Louis, 1904, Vol. I, p. 130.
[38] Annuaire pour l'an 1913, Paris. Gauthier- Villars
[39] Heaviside, O. "The Electrician," 1884, May 3, p. 583; also "Electrical Papers”, Macmillan Co 1892, Vol 1, p.354.
[40] Heaviside, O. " Electrical Papers," 1892, Vol II, pp. 302 and 327
[44] Maxwell, J. C. "A Treatise on Electricity and Magnetism." 1881, Vol II, p244.
[50] Rucker. Phil. Mag., Feb., 1889.